Лабораторная работа № 80

ИССЛЕДОВАНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА

Цель работы: изучение дифракции Фраунгофера на одной щели, на двух щелях, на четырех щелях, на одномерной дифракционной решетке в монохроматическом свете от лазерного источника.

Приборы и принадлежности: Модульный учебный комплекс МУК – 0.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

1.1. Дифракция света. Принцип Гюйгенса – Френеля

Дифракцией называется совокупность явлений, наблюдаемых при прохождении света в среде с резкими неоднородностями (малыми отверстиями, непрозрачными экранами и т.п.) и связанных с отклонениями от прямолинейности распространения. Дифракция приводит к огибанию световыми волнами препятствий, проникновению света в область геометрической тени. Отклонение света от прямолинейности распространения можно объяснить с помощью принципа Гюйгенса – Френеля. Согласно этому принципу каждая точка, до которой доходит волна, служит источником вторичных элементарных сферических волн, а их огибающая определяет положение волнового фронта (поверхность, отделяющая часть пространства, вовлеченную в волновой процесс, от области в которой колебания еще не возникли) в следующий момент времени. Эти источники когерентны (колебания всех точек волнового фронта происходят с одинаковой частотой и в одинаковой фазе), волны, исходящие из них, также когерентны и интерферируют при наложении.

Каждая из вторичных волн возбуждает в точке наблюдения колебания, амплитуда результирующего колебания равна векторной сумме амплитуд складываемых колебаний. Результат сложения зависит от разности фаз , приходящих в точку наблюдения волн. В свою очередь  связана с оптической разностью хода  волн

   .                                       (1.1)

Если оптическая разность хода равна целому числу длин волн (, m=0,1,2,3…), то фазы приходящих в точку наблюдения волн одинаковы

.                                    (1.2)

Они усиливают друг друга, возникает максимум интенсивности света. Если же разность хода равна полуцелому числу длин волн,

, то волны встречаются в противофазе

  .                               (1.3)

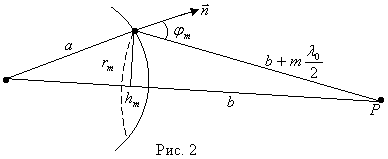
Они ослабляют друг друга, образуется минимум интенсивности света.

Таким образом, при распространении световых волн от источника свет будет наблюдаться только в тех точках пространства, где вторичные волны при интерференции усиливают друг друга.

1.2. Метод зон Френеля

В общем случае расчет интерференции вторичных волн представляет собой сложную математическую задачу. Метод зон Френеля позволяет значительно упростить ее. Для пояснения сути метода определим амплитуду светового колебания, возбуждаемого в точке Р сферической волной, распространяющейся в изотропной однородной среде из точечного источника S (рис 1).

В соответствии с принципом Гюйгенса – Френеля все точки неограниченного волнового фронта Ф (сферической поверхности радиуса а) являются источниками вторичных сферических волн. Разобьем волновую поверхность Ф на кольцевые зоны (зоны Френеля) таким образом, чтобы расстояние от краев соседних зон до Р отличались на .

 .                      (1.4)

Тогда исходящие из двух симметричных источников соседних зон волны возбуждают в точке Р колебания, отличающиеся на . Суммарные колебания, обусловленные действием соседних зон Френеля, находятся в противофазе и ослабляют друг друга.

Амплитуда результирующего колебания в точке Р будет равна

 ,                  (1.5)

где А₁, А₂, …, А_m – амплитуды колебаний, возбуждаемых 1-й, 2-й, …, m-й зонами Френеля.

Амплитуда колебаний А_m, обусловленная действием m-й зоны Френеля, зависит от ее площади, номера m и угла  (рис.2).

Как показывает расчет, площади всех зон Френеля примерно одинаковы, действие же зоны уменьшается с ростом m, т.к. при этом увеличивается расстояние от зоны до точки Р. Одновременно растет угол , что также ослабляет действие зоны (ее излучение максимально в направлении нормали ). Все это приводит к тому, что амплитуда А_m монотонно убывает по мере роста номера m.

Таким образом, амплитуды колебаний, приходящих со всех зон Френеля в точку Р, образуют монотонно убывающую последовательность

Суммарную амплитуду (1.5) можно представить в виде

   (1.6)

Вследствие монотонного убывания А_m можно приближенно

считать, что  .

Тогда выражения в скобках будут равны 0, и с учетом того, что для больших m величиной  можно пренебречь, формула (1.6) примет вид

.                                        (1.7)

Найдем радиус m-й зоны Френеля. Из рис. 2 видно, что

.

С учетом того, что ,  и , получим 

,    ,       .      (1.8)

Длина световой волны весьма мала ( для зеленого света). Приняв а=b=1м, получим радиус первой зоны Френеля . Следовательно, распространение света от S к Р происходит так, как если бы  световой поток шел внутри узкого канала, т.е. прямолинейно.

Описанный метод позволяет также объяснить дифракцию света на различных резких неоднородностях (малых отверстиях, непрозрачных экранах).

Различают дифракцию Френеля и Фраунгофера. Дифракцию Френеля (дифракция сферических волн) наблюдают при конечных расстояниях от источника света до препятствия и от препятствия до точки наблюдения. Дифракция Фраунгофера (дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точка наблюдения достаточно удалены от преграды, вызывающей дифракцию.

1.3. Дифракция Фраунгофера на узкой щели

Пусть плоская монохроматическая волна падает нормально на щель шириной а. Когерентные вторичные волны распространяются от нее по всем направлениям. Результат их интерференции можно наблюдать на экране Э, расположенном в фокальной плоскости (рис 3) линзы Л.

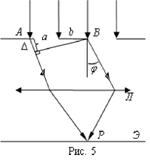
Оптическая разность хода волн, идущих от краев щели в произвольном направлении , равна

.                                       (1.9)

После прохождения через линзу Л они собираются на экране в точке Р и интерферируют. Для выяснения вида интерференционной картины разобьем открытую поверхность волнового фронта АВ на зоны Френеля (разность хода от краев соседних зон равна ), параллельные краям щели. Всего на ширине  щели уместится

  зон.                               (1.10)

Так как на щель падает плоская волна, то площади всех зон одинаковы,  значит, одинакова амплитуда колебаний, возбуждаемых в точке Р действием каждой зоны Френеля, а фазы колебаний, создаваемых соседними зонами, противоположны. Следовательно, колебания каждой пары соседних зон будут гасить друг друга.

Поэтому, если на ширине щели укладывается четное число зон Френеля, то амплитуда результирующего колебания в точке Р равна 0 и наблюдается минимум интенсивности света.

Из (1.10) следует условие образования дифракционного минимума:

 (k=1,2,…)                      (1.11)

Дифракционный максимум возникает при нечетном числе зон Френеля, укладывающихся на ширине щели

 (k=1,2,…),                       (1.12)

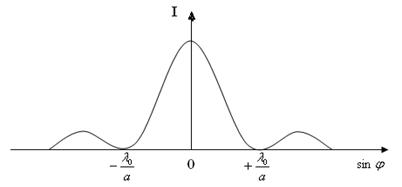
где k определяет порядок дифракции.

В этом случае действие щели эквивалентно действию одной зоны Френеля, поскольку действие остальных пар зон взаимно компенсируется.

Волны, распространяющиеся от щели в прямом направлении (, возбуждают в точке О экрана колебания, усиливающие друг друга, т.к. все они приходят в одинаковой фазе (). В этой точке возникает самый интенсивный центральный дифракционный максимум (k=0).

Итак, волны, дифрагирующие от щели под углами, соответствующими нечетному числу зон Френеля, создают на экране максимумы интенсивности света, а волны, дифрагирующие под углами, соответствующими четному числу зон Френеля, - минимумы.

В целом дифракционная картина, возникающая при прохождении монохроматического света через узкую щель, имеет вид чередующихся светлых и темных полос, симметрично расположенных по обе стороны от центральной светлой полосы.

Выражение (1.11) позволяет найти угловое положение первого минимума (k=1) (рис.4).

,                                    (1.13)

а минимальное число полос определяется требованием

, .                                  (1.14)

Из выражений (1.13) и (1.14) следует, что сужение щели приводит к тому, что центральный максимум расплывается (яркость уменьшается).

Это относится и к другим максимумам, картина становится менее четкой. При  минимумы вообще не возникают, интенсивность света монотонно убывает от середины картины к ее краям. Наоборот, чем шире щель (), тем картина ярче, дифракционные полосы уже, а число полос больше. При  в центре получается яркое изображение щели, т.е. имеет место прямолинейное распространение света.

1.4. Дифракционная решетка

При дифракции от одной щели интенсивность света в максимумах невелика и дифракционная картина недостаточно четко выражена. Для получения картины с четкими максимумами интенсивности света применяется дифракционная решетка.

Одномерная дифракционная решетка – это система параллельных щелей равной ширины а, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками b. Величина

                                      (1.15)

называется постоянной (периодом) дифракционной решетки.

При падении на решетку плоской монохроматической волны в фокальной плоскости линзы наблюдается дифракционная картина.

одна из щелей не распространяет света, он не будет распространяться и при двух щелях, т.е. прежние минимумы интенсивности будут возникать в направлениях, определяемых условием (1.11)

 (k=1,2,…).

Кроме того, в некоторых других направлениях вторичные волны, идущие от двух щелей, будут гасить друг друга вследствие интерференции, т.е. будут наблюдаться дополнительные минимумы. Они возникают в направлениях, отвечающих условию

        (m=0,1,2,…),               (1.16)

где  - разность хода лучей, идущих от краев А и В щелей. Действие одной щели будет усиливать действие другой, если в разности хода укладывается целое число длин волн:

 (m=0,1,2,…).            (1.17)

Формула (1.17) – условие образования главных максимумов.

Все волны, распространяющиеся за щелями в прежнем направлении (), создают центральный максимум (m=0). Таким образом, полная дифракционная картина от двух щелей определяется условиями образования:

прежних минимумов

дополнительных минимумов

главных максимумов

Следовательно, между двумя главными максимумами располагается один добавочный минимум. Это приводит к тому, что максимумы становятся более узкими, чем при одной щели.

Если решетка содержит N щелей, то между двумя главными максимумами расположатся (N-1) дополнительных минимумов, разделенных слабыми вторичными максимумами в количестве (N-2). При этом прежними остаются условия образования прежних минимумов (1.11) и главных максимумов (1.17).

На рис.6 для примера приведена дифракционная картина, наблюдаемая для N=4 и d/a=3. В данном случае главные максимумы третьего, шестого и т.д. порядков приходятся на минимумы интенсивности от одной щели, в результате чего они не наблюдаются. Штриховая линия задает распределение интенсивности при дифракции от одной щели, умноженной на N², так как I_max в N² раз больше интенсивности, создаваемой в направлении φ одной щелью.

Как видно, четкие главные максимумы разделены темными пространствами.  Чем больше щелей N содержит решетка, тем больше количество световой энергии пройдет через нее, тем больше минимумов образуется между соседними главными максимумами, тем более интенсивными и острыми будут максимумы. В итоге дифракционная картина от решетки с достаточно большим числом щелей представляет собой систему узких ярких полос, разделенных сравнительно темными промежутками.

Положение главных максимумов зависит, как видно из (1.17), от длины волны  . Поэтому при пропускании  через решетку белого света все максимумы, кроме центрального (m=0), разложатся в спектр (m – порядок спектра), фиолетовая область которого обращена к центру дифракционной картины, красная – наружу.

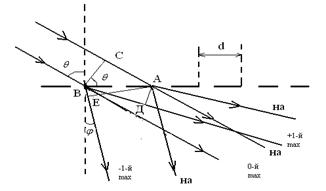
В центре белая полоса, т.к. центральный максимум образован недифрагированными волнами, для которых разность хода равна 0 и условие возникновения максимума одинаково для всех длин волн. Из (1.17) следует, что чем выше порядок спектра, тем больше угол дифракции, соответствующий образованию максимума, тем шире спектр. Это приводит к частичному перекрытию спектров, начиная со спектров 2-3 порядков.

1.5. Наклонное падение лучей

Если плоская волна падает на решетку наклонно под углом q, то разность хода между соседними пучками становятся равной АС-ДВ=d sinq-sin (рис. 7).

Рис. 7

Характер дифракционной картины в основном сохраняется. Положение главных максимумов определяется условием

d(sin                             (1.18)

 - направление на главный максимум порядка m
(m=0,).

Преобразуем соотношения 1.18, воспользовавшись тригонометрической формулой разности синусов двух углов, т.е.

sin.              (1.19)

С учетом 1.19 формула 1.18 преобразуется к виду

                (1.20)

Если решетка довольна груба, т.е. период ее d значительно больше , то углы дифракции малы и угол  мало отличается от . В таком случае можно положить:

 и         (1.21)

С учетом (1.21) формула (1.20) принимает вид:

                              (1.22)

Сравним формулу 1.22 с формулой для нормального падения волнового фронта на решетку dsin или d, если угол  мал. Это сравнения показывает, что угол между направлениями на нулевой максимум и на ненулевые максимумы () вычисляется так же, как если бы падение было нормальным, но решетка имела бы уменьшенный период, а именно . Следовательно, роль периода решетки d играет величина dcos, которая может быть сделана очень малой. Скользящее падение лучей как бы уменьшает период решетки и увеличивает углы дифракции. Таким путем удается получать отчетливые дифракционные спектры даже от очень грубых решеток, например от граммофонных пластинок. Последние позволяют в демонстрационной аудитории получать в белом свете довольно красивые дифракционные спектры разных порядков.

Метод скользящего падения имеет большое значение в ренгеновской спектроскопии при исследовании дифракции рентгеновских лучей.

2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ

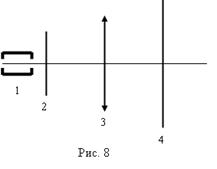
Схема установки для исследования дифракции Фраунгофера представлена на рис. 8, где 1 – источник плоской монохроматической световой волны (лазер); 2 – набор щелей; 3 – линза, в фокальной плоскости которой расположен экран 4 (съемный лист белой бумаги).

Внешний вид установки МУК – 0 изображен на рис. 9,

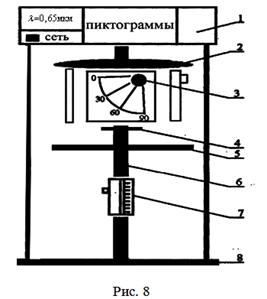
где:

1 – устройство с полупроводниковым лазерным осветителем;

2 – турель, на которой смонтированы объекты исследования для лабораторных работ по интерференции и дифракции;

3 – диафрагма;

4 – поляризатор, закрепленный на турели во вращающейся обойме со стрелкой – указателем и транспортиром;

5 – турель с объектом исследования, используемым в работах по поляризации света;

6 – стойка;

7 – устройство, содержащее поворотную стеклянную пластинку, использующуюся в опытах по изучению закона Брюстера;

8 – основание оптического блока.

Лазерный источник света находится в верхней части установки. Ниже расположенная турель содержит все объекты исследования: одна щель, две щели, четыре щели, одномерная дифракционная решетка.

Рекомендуется вначале провести измерения с одиночной щелью, установив ее  (см. пиктограмму) под лазерным источником. Затем, вращая турель, переходить к двум, четырем щелям и одномерной решетке, место расположения которой определяется также по соответствующим пиктограммам.

Если на пути лазерного пучка поставить щель, то на экране Э за щелью будет наблюдаться дифракционная картина в виде центрального наиболее яркого максимума и системы расположенных симметрично ему максимумов различных порядков, разделенных минимумами (рис. 10).

Угловое положение минимумов определяется соотношением (1.11) . Учитывая , что углы дифракции в этом случае

малы, получим .

Тогда

,                                                (2.1)

где  - расстояние от центра дифракционной картины до минимума k-ого порядка. При переходе от минимума порядка k к минимуму порядка (k+1) получим

.                                        (2.2)

Разность

                                     (2.3)

называется шириной дифракционной полосы.

Таким образом, используя явление дифракции, можно по формуле (2.3) определить размеры щелей и препятствий.

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
   И ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

3.1. Включите лазерный монохроматический источник света ( мкм, что соответствует красному видимому свету), тумблером «сеть».

3.2. Положите лист белой или миллиметровой бумаги на основание оптического блока (8).

3.3. Поверните турель 2 и установите первый объект исследования- одиночную щель в положение, перпендикулярное направлению светового пучка.

3.4. С помощью ручки 3 установите стрелку, закрепленную на оси вращения пластинки со щелью, на угол 0. Объекты 4 и 5, не используемые при изучении дифракции света, выведите из под светового пучка.

3.5. На бумаге должна появиться дифракционная картина – ряд чередующихся красных полосок (см. рис. 11).

3.6. Зарисуйте дифракционную картину.

3.7. По своему рисунку измерьте положение минимума первого порядка х (см. рис. 11). Результат запишите в таблицу.

3.8. По формуле  рассчитайте ширину щели . Расстояние L указано на передней панели установки (L = 465 мм).

3.9. Повторите опыт несколько раз.

3.10. Ручкой 3 поверните щель на угол 30 по отношению к первоначальному положению. Пронаблюдайте изменения дифракционной картины и зарисуйте ее. Объясните увиденное.

3.11. Поверните турель 2, установите на место одиночной щели пластину с двумя щелями. С помощью ручки 3 установите угол 0 и зарисуйте дифракционную картину.

3.12. На своем рисунке измерьте координату максимума первого порядка  и по форме  найдите расстояние d между щелями. Результаты занесите в таблицу.

3.13. Ручкой 3 поверните пластину со щелями на углы  и зарисуйте дифракционные картины. Результаты занесите в таблицу.

3.14. Вычислите расстояние d, пользуясь результатами этих опытов.

3.15. Повторите аналогичные опыты для четырех щелей и для одномерной дифракционной решетки.

3.16. Результат измерений и вычислений занесите в таблицу.

Рис. 11

Таблица результатов

4. ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

1.      Сформулируйте цель работы.

2.      Объясните сущность дифракции света.

3.      Опишите порядок выполнения работы.

5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.      Сформулируйте принцип Гюйгенса – Френеля. Объясните с его помощью явление дифракции света.

2.      Метод зон Френеля.

3.      Объясните картину дифракции на одной щели.

4.      Почему изменяются положения максимумов и минимумов при повороте объектов исследования по отношению к падающему на них световому пучку?

5.      Получите условия минимумов и максимумов при дифракции на одномерной решетке.

ЛИТЕРАТУРА

1.      И.В. Савельев. Курс общей физики, М.: Наука, 1987.    – т.2

2.      Б.М. Яворский, А.А. Детлаф. Курс физики, М.: Высшая школа, 1972.    – т.3

3.      Лабораторный практикум по физике под ред. К.А. Барсукова и Ю.И. Уханова. М.: высшая школа, 1988.    - 350 с.

4.      Н.М. Годжаев. Оптика, М.: Высшая школа, 1977.    - 430 с.

5.      Г.С. Ландсберг. Оптика, М.: Наука, 1976.   - 926 с.