Лабораторная работа № 61

ИЗУЧЕНИЕ ЗРИТЕЛЬНОЙ ТРУБЫ

Цель работы: определение увеличения зрительной трубы и измерение ее предела разрешения.

Приборы и принадлежности: оптическая скамья ОСК-2; осветитель с конденсором, лампой накаливания 8В и матовым стеклом; зрительная труба; револьвер с мирой.

1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

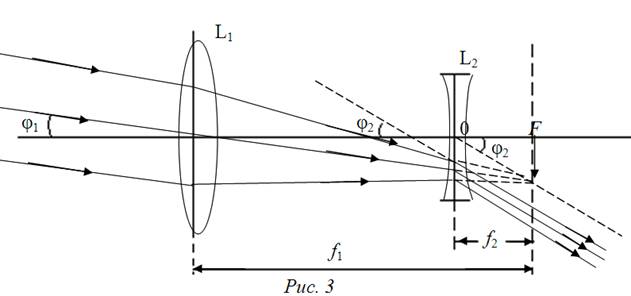
Зрительная труба представляет собой оптический прибор, предназначенный для рассматривания глазом весьма удаленных предметов. Она состоит из объектива и окуляра, которые являются сложными оптическими системами; однако мы их будем схематически представлять тонкими линзами. В зрительных трубах объектив и окуляр располагаются так, что задний фокус объектива F₁^/ приближенно совпадает с передним фокусом окуляра F₂ (рис. 1).

На рис. 1: D₁ – диаметр объектива; D₂ – диаметр окуляра;
f₁, f₂ – фокусные расстояния объектива и окуляра.

Объектив дает действительное уменьшенное обратно изображение бесконечно удаленного предмета в своей задней фокальной плоскости. Это изображение рассматривается в окуляр, как в лупу. Если передний фокус окуляра совпадает с задним фокусом объектива, то при рассматривании удаленного предмета из окуляра выходят пучки параллельных лучей, что удобно для наблюдения нормальным глазом в спокойном состоянии (без аккомодации). Но если  зрение наблюдателя несколько отличается от нормального, то окуляр передвигают, устанавливая его «по глазам». Путем передвижения окуляра производится также «наводка» зрительной трубы при рассматривании предметов, расположенных на различных не очень больших расстояниях от наблюдателя.

Объектив зрительной трубы должен быть всегда собирательной системой, окуляр же может быть как собирательной, так и рассеивающей системой. Зрительная труба с собирательным (положительным) окуляром называется трубой Кеплера. Ход лучей в зрительной трубе Кеплера изображен на рис. 2.

Объектив L₁ дает действительное обратное изображение удаленного предмета в своей фокальной плоскости FЕ. Расходящийся пучок лучей из точки Е падает на окуляр L₂. Так как эти лучи идут из точки Е в фокальной плоскости окуляра, то из него выходит пучок, параллельный побочной оптической оси ЕО окуляра. Попадая в глаз (А), лучи эти сводятся на его сетчатке и дают действительное изображение источника. В трубе Кеплера расстояние между объективом и окуляром равно сумме их фокусных расстояний (рис. 2).

Зрительная труба с рассеивающим (отрицательным) окуляром называется трубой Галилея. Труба Галилея дает прямое изображение объекта, причем расстояние между объективом и окуляром равно разности их фокусных расстояний. Ход лучей в зрительной трубе Галилея изображен на рис. 3.

В случае галилеевой трубы глаз не изображен, чтобы не загромождать рисунка. Пусть пучок света, падающий в объектив, составляет с оптической осью угол j₁, а пучок, выходящий из окуляра, –
угол j₂, причем j₂ > j₁.

Увеличение зрительной трубы определяется соотношением

.                                                 (1)

Из рис. 2 видим

,                                              (2)

где f₁ – фокусное расстояние объектива; f₂ – фокусное расстояние окуляра.

Из рис. 1 –

,                                                  (3)

где D₁ – диаметр объектива зрительной трубы; D₂ – диаметр изображения объектива в окуляре.

Объединяя (1), (2), (3), для увеличения g найдем формулу

.                              (4)

Соотношение (4) показывает, что увеличение трубы можно определить следующими тремя способами: путем измерения углов, под которыми предмет виден без трубы и через трубу; путем измерения диаметров объектива и его изображения в окуляре; путем измерения фокусных расстояний объектива и окуляра.

При рассмотрении вопроса о возможности различения с помощью зрительной трубы мелких деталей предмета необходимо учитывать дифракционные явления, которые определяют разрешающую
силу зрительной трубы, т.е. возможность получения раздельных изображений двух близких точек предмета. Свет, попадающий в зрительную трубу, дифрагирует на круглой оправе объектива, играющей роль входного зрачка системы, в результате чего в фокальной плоскости объектива получается не простое сигматическое изображение точки, а сложная дифракционная картина с центральным максимумом освещенности, окруженным темными и светлыми кольцами. Причем радиус первого темного кольца определяется формулой

,                                            (5)

где D – диаметр входного зрачка – оправы или диафрагмы объектива; λ – длина волны падающего света;  f₁ – фокусное расстояние объектива.

Если объектив направлен на две удаленные звезды, разделенные угловым расстоянием dj, то каждая из них даст в фокальной плоскости дифракционные кружки с центром в точках, соответствующих изображениям звезд (рис. 4).

Дифракционные картины от двух очень близких звезд частично перекроются и возникнет одно более или менее удлиненное и неоднородное по освещенности светлое пятно. В каком случае это пятно может еще восприниматься как изображение двух звезд и в каком – уже нельзя будет утверждать, что оно образовано двумя, а не одной звездой?

По Релею, для определенности принимают за предел разрешения такое положение, при котором максимум освещенности дифракционной картины от одной точки предмета совпадает с первым минимумом освещенности дифракционной картины от его второй точки (рис. 5), т.е. такое положение, при котором первое темное кольцо одного кружка проходит через светлый центр второго. Тогда наименьшее расстояние между разрешаемыми изображениями точек будет равно величине радиуса первого темного кольца. Предельное угловое расстояние j между еще разрешаемыми объективом точками объекта (рис. 4) определится соотношением

,                                                               (6)

где r₁ – радиус первого темного кольца; f₁ – фокусное расстояние объектива.

Подставив выражение (6) в (5), получим

j =  1,22 радиан 

j =  1,22 · 2 · 10⁵  угловых секунд.                   (7)

Из равенства (7) видно, что чем больше диаметр объектива, тем более близкие точки он позволяет разрешить.

Величина, обратная предельному углу, носит название разрешающей силы объектива:

.                                       (8)

Окуляр трубы на ее разрешающую силу на влияет.

Для определения разрешающей силы объективов зрительных труб пользуются специальными штрихованными таблицами – мирами (рис. 6). Мира представляет собой негативное изображение таблицы, изготовленное фотографическим способом на мелкозернистой коллоидной пластинке. Мира состоит из 25 элементов, отличающихся между собой шириной нанесенных штрихов. Каждый из элементов состоит из четырех квадратов (ширина квадрата 0,4 мм). Штрихи в каждом квадрате расположены в четырех различных направлениях: горизонтальном, вертикальном, с наклоном вправо и влево под углом 45°. Штрихи должны быть абсолютно белыми на черном фоне или черными на светлом фоне. Ширина штрихов в пределах одного элемента должна быть постоянной. Расстояние между штрихами в каждом квадрате равно ширине штриха. Ширина штрихов уменьшается от элемента 1 к элементу 25 по закону геометрической прогрессии со знаменателем . На рис. 6 приведены квадраты с наиболее крупными штрихами

миры.

Миры различают по номерам. Отечественная промышленность выпускает стандартные штриховые миры шести номеров (см. табл. 1), которые отличаются числом штрихов в элементах и базой миры В (В – расстояние между базовыми штрихами, которые на рисунке 6 показаны черточками).

Таблица 1

Предельное угловое расстояние j между еще разрешаемыми точками объекта наблюдения вычисляют по формуле

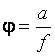 радиан = 2 · 10⁵ угловых секунд,                       (9)

где  – ширина штриха для номера элемента N данной миры, в пределах которого штрихи еще наблюдаются разрешенными; f – фокусное расстояние объектива коллиматора.

Разрешающую способность R_N, выраженную числом штрихов на 1 мм, для любого номера N данной миры вычисляют по формуле

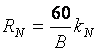,                                              (10)

где В – база миры, мм; k_N – коэффициент, зависящий от номера элемента, k_N = 1,06 ^N–1; 60 – число, принятое для вычисления разрешающей способности.

2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ

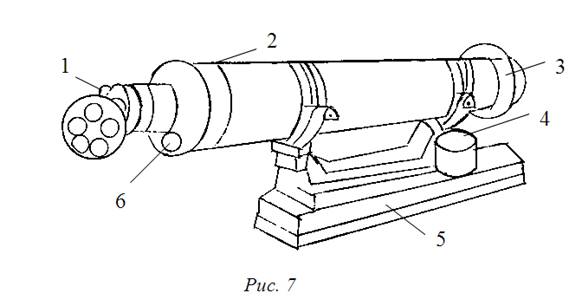
В данной работе используется оптическая скамья ОСК-2 (рис. 7), коллиматор которой имеет фокусное расстояние f₁ = 1 600 мм.

На рис. 7: 1 – винт поворота коллиматора в горизонтальной плоскости; 2 – маховичок поворота коллиматора в вертикальной плоскости; 3 – объектив; 4 – колпачок для предохранения объектива от пыли; 5 – станина; 6 – маховичок фокусировки.

Объектив коллиматора 1 должен быть строго отфокусирован, т.е. установлен на бесконечность.

Установка по методу автоколлимации наиболее точная и удобная в лабораторных условиях. При использовании автоколлимационного метода необходимы плоскопараллельная стеклянная пластинка и автоколлимационный окуляр (или окуляр и сетка с призмой). Установить плоскопараллельную пластинку перед объективом коллиматора 1 на дополнительном столике. Сетку с призмой и окуляр вставить в коллиматор. Произвести подсветку сетки и, наблюдая в окуляр, поймать резкое отражение от плоскопараллельной пластинки изображения сетки. Фокусировку коллиматора осуществлять вращением маховичка механизма фокусировки коллиматора 4. Отсчет вести по линейной шкале и нониусу механизма фокусировки.

После того, как будет получено резкое отражение изображения сетки, заметить деление по шкале механизма фокусировки коллиматора – это деление и будет соответствовать положению объектива коллиматора, установленного на бесконечность (это деление надо искать в интервале цифры 50 ± 5 делений, а при работе с приспособлением для автоколлимации в виде кубика это деление надо искать в интервале цифры 38 ± 5 делений).

Оставив коллиматор в положении, выставленном на «бесконечность», вынуть сетку с призмой и окуляр, а вместо них поставить револьвер с мирой так, чтобы торец револьвера вплотную прилегал к срезу трубы. Это соответствует положению миры в фокусе коллиматора.

Для проведения измерений на оптической скамье (рис. 7) располагают осветитель с матовым стеклом, коллиматор с мирой, испытуемую зрительную трубу (рис. 8). Миру помещают в фокусе линзы коллиматорной трубы. Зрительную трубу устанавливают объективом как можно ближе к объективу коллиматора.

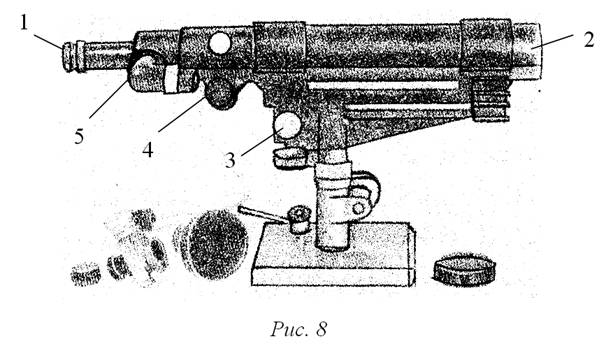
На рис. 8: 1 – окуляр, 2 – объектив, 3 – винт для перемещения по вертикали, 4 – винт фокусировки, 5 – патрон освещения.

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
И ОБРАБОТКА РЕЗУЛЬТАТОВ

Упражнение 1. Определение увеличения зрительной трубы.

3.1.1. Включают осветитель.

3.1.2. Устанавливают позади окуляра зрительной трубы рейтер с матовым стеклом.

3.1.3. Передвигая рейтер с матовым стеклом, находят такое положение, при котором на матовом стекле отчетливо видно резко очерченное круглое светлое пятно – изображение оправы объектива.

3.1.4. Измеряют диаметр объектива зрительной трубы и диаметр его изображения.

3.1.5. По формуле 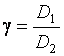, где D₁ – диаметр объектива зрительной

трубы; D₂ – диаметр изображения объектива в окуляре, вычисляют увеличение зрительной трубы.

3.1.6. Сравнивают результат, найденный опытным путем, с теоретическим значением, рассчитанным по формуле (4): ,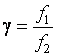

где f₁ = 430 мм – фокусное расстояние объектива зрительной трубы;
f₂ = 21,5 мм – фокусное расстояние окуляра зрительной трубы.

3.1.7. Вычисляют относительную погрешность. Результаты измерений и вычислений заносят в таблицу (форма табл. 2).

Форма таблицы 2

Упражнение 2. Определение разрешающей способности объектива зрительной трубы.

3.2.1. Миру помещают в фокусе линзы коллиматорной трубы. Через зрительную трубу, установленную как можно ближе к объективу коллиматора, рассматривают изображение штрихов миры, предельно разрешаемых объективом трубы по всем четырем направлениям. В работе используется мира № 5 с базисом В = 19,2 мм.

3.2.2. Определяют число штрихов в первом элементе (квадрате) миры.

3.2.3. Зная ширину элемента (0,4 мм) и число штрихов в нем, находят ширину штрихов  в этом элементе.

3.2.4. Определяют ширину штрихов для 5, 10, 15, 20 и 25-го элементов, учитывая, что ширина штрихов уменьшается от элемента 1 к элементу 25 по закону геометрической прогрессии со знаменателем .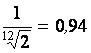

3.2.5. По формуле (9) рассчитывают угловое расстояние j между разрешаемыми точками объекта наблюдения для пятого, десятого, пятнадцатого, двадцатого и двадцать пятого элементов миры № 5, где f = 430 мм – фокусное расстояние объектива зрительной трубы.

3.2.6. Сравнивают результаты, полученные опытным путем, с теоретическими (табл. 3).

Таблица 3

Окончание табл. 3

3.2.7. Вычисляют относительную погрешность. Результаты измерений и вычислений заносят в таблицу (форма табл. 4).

Форма таблицы 4

3.2.8. По формуле (10) рассчитывают разрешающую способность объектива зрительной трубы для 1, 5, 10, 15, 20, 25-го элементов миры № 5. Результаты вычислений заносят в таблицу (форма табл. 4) и сравнивают с результатом табл. 1.

ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

1. Сформулируйте цель работы.

2. Для чего предназначена зрительная труба и из каких основных частей она состоит?

3. Каковы методы определения увеличения зрительной трубы?

4. Как оценить разрешающую способность объектива зрительной трубы?

ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.       Опишите ход лучей в зрительных трубах Кеплера и Галилея.

2.       Что понимается под разрешающей способностью и критерием Релея?

3.       Что представляет собой мира и для чего она используется?

ЛИТЕРАТУРА

1. Ландсберг Г.С. Оптика.– М.: Наука, 1976.

2. Физический практикум / Под ред. В.И. Ивероновой.– М.: Наука, 1968.

3. Гвоздева Н.П., Коркина К.И. Прикладная оптика и оптические измерения.– М.: Машиностроение, 1976.

4. Тудоровский А.И. Теория оптических приборов.– М.: Изд-во АН СССР, 1937.