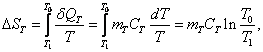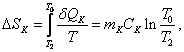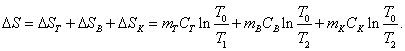Лабораторная работа № 210

ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ РЕАЛЬНЫХ

СИСТЕМ

Цель работы:  на основании II закона термодинамики, используя экспериментальные данные, определить изменение энтропии реальных тел.

Приборы и принадлежности:

калориметрический стакан,

термометр,

нагреватель,

набор различных тел,

мерный стакан.

1.      ЗАКОНЫ ТЕРМОДИНАМИКИ

Термодинамика – наука о наиболее общих тепловых свойствах макроскопических тел. Термодинамика изучает процессы превращения энергии из одного вида в другой и характеризует эти превращения с количественной стороны. Она занимается изучением различных свойств тел и изменений состояния вещества на макроскопическом уровне.

В основе термодинамики лежат три фундаментальных закона (три начала термодинамики), установленных на основании обобщения большой совокупности опытных данных. Мы в этой работе ограничимся рассмотрением только двух законов термодинамики.

I закон термодинамики выражает всеобщий закон сохранения и превращения энергии и гласит, что количество теплоты, сообщаемое термодинамической системе, расходуется на увеличение внутренней энергии и на совершение системой работы против внешних сил. Математическая запись I закона термодинамики:

                                                            (1)

где dU – бесконечно малое изменение внутренней энергии системы; dQ, dA – соответственно, бесконечно малая теплота, подводимая к системе и элементарная работа.

     Термодинамической системой называется совокупность макроскопических объектов (тел), обменивающихся энергией и веществом друг с другом и с внешней средой. Состояние термодинамической системы характеризуется температурой Т, давлением Р, объемом V, массой m и другими величинами, которые называются термодинамическими параметрами. Термодинамические системы, которые не обмениваются с внешней средой ни энергией, ни веществом, называются изолированными (замкнутыми).

Всякое изменение состояния термодинамической системы, связанное с изменением ее параметров состояния, называется термодинамическим процессом. I закон термодинамики не позволяет определить направление протекания термодинамических процессов в природе. Например, если происходит теплообмен между телами различной температуры, то закон сохранения энергии требует только, чтобы количество теплоты, отданное одним телом, равнялось количеству теплоты, полученному другим. То есть ответить на вопрос, в каком направлении происходит переход теплоты, первый закон термодинамики не может. Первому закону термодинамики не противоречит самопроизвольный процесс перехода теплоты от тела менее нагретого к телу более нагретому. В природе самопроизвольный процесс перехода теплоты происходит только от тела более нагретого к телу менее нагретому. I закон термодинамики не может дать ответ на вопрос, возможен ли в тепловой машине полный переход теплоты в работу? Из опыта известно, что работа полностью может перейти в теплоту, а обратный процесс возможен только при Т = const. Как показал Карно, превращение теплоты в работу подвержено ограничению: необходимым условием такого превращения является разность температур, и чем она больше, тем большая доля теплоты может превратиться в работу. Тепловые машины дают возможность превращать теплоту в работу, однако не в эквивалентных количествах, поскольку КПД машин всегда меньше единицы. Поэтому теплота, которая берется от нагревателя, больше теплоты, превращаемой в работу, и часть ее отдается холодильнику. Можно привести и другие примеры.

Ответы на выше поставленные вопросы дает II закон термодинамики. Существует несколько формулировок II закона термодинамики, отличающихся по форме, но одинаковых по существу.

Согласно Карно: «Теплота не может самопроизвольно перейти от холодного тела к горячему».

По Клаузиусу: «Невозможны такие процессы, единственным результатом которых был бы переход теплоты от тела менее нагретого к телу более нагретому». Для такого перехода теплоты требуется затрата работы от внешнего источника.

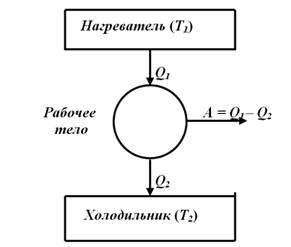
Физический смысл II закона термодинамики наиболее ясно раскрывается в формулировке Томсона и Планка: «Невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты, полученной от нагревателя, в эквивалентную ей работу».                         

Возможным является такой периодический процесс, при котором часть теплоты Q₁, полученной рабочим телом от нагревателя, превращается в работу, а другая часть теплоты Q₂  не используется и передается холодильнику с температурой Т₂<T₁ (рис. 1).

Таким образом, в любой тепловой машине превращается в работу только часть полученной от нагревателя теплоты:

А = Q₁ - Q₂.

Формулировка  второго закона термодинамики по Оствальду: «Невозможно осуществить вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара энергии и полностью превращал это тепло в работу».

                                                       Рис. 1. 

Итак, из вышеперечисленных формулировок видно, что II закон термодинамики указывает направление самопроизвольных термодинамических процессов и налагает ограничение на возможность превращения тепла в работу.

Круговые процессы (циклы), при протекании которых в окружающей среде остаются какие-либо изменения, называются необратимыми. Необратимые процессы могут самопроизвольно протекать только в одном направлении. Например, необратимыми являются: переход тепла от нагретого тела к холодному, диффузия, расширение газа в пустоту, выравнивание температуры и т.д. Практически все явления природы являются необратимыми из-за наличия диссипативных сил, диффузии и др.

В природе любая изолированная система через достаточно длительный промежуток времени переходит в равновесное состояние. Если при постоянных внешних условиях параметры состояния термодинамической системы во всех ее частях при одинаковой температуре не меняются со временем, а также отсутствуют потоки энергии, импульса, массы вещества, то такое состояние называется равновесным. В равновесном состоянии изолированная система может находиться сколь угодно долго и сама по себе не может выйти из этого состояния.

Обратимым процессом называется такой процесс, в результате которого вся система возвращается в первоначальное состояние без каких-либо изменений в окружающей среде. Примером обратимых процессов являются все механические процессы, если в них нет превращения механической энергии в другие виды энергии (электромагнитную, тепловую и т.д.), т.е. если отсутствуют диссипативные силы.

На практике обратимый процесс неосуществим, он является абстракцией реального процесса. Хотя в природе не существуют обратимые процессы, однако их изучение дает возможность понять основные термодинамические свойства реальных систем.

В современной термодинамике для формулировки второго закона термодинамики используется понятие энтропии S, введенное Клаузиусом.

Как известно, при сохранении внутренней энергии в изолированной термодинамической системе, казалось бы, возможны любые процессы. На самом деле не совсем так. Дело в том, что различные состояния, отвечающие одной и той же энергии, обладают разной вероятностью. Изолированная система будет самопроизвольно переходить из менее вероятных в более вероятные состояния, либо длительное время будет находиться в равновесном (более вероятном) состоянии.

Рассмотрим пример. Пусть изолированная система состоит из двух тел с различной температурой в начальный момент времени. В ней будет протекать процесс теплопередачи, приводящий к выравниванию температуры. После того, как температура обоих тел станет одинаковой, система будет оставаться в таком состоянии неограниченно долго. Поэтому в изолированной системе невозможен процесс, в результате которого температура одного из одинаково нагретых тел стала бы больше или меньше другого.  Можно привести другой пример: процесс распространения газа на весь сосуд. Обратный процесс, в результате которого газ самопроизвольно собрался бы в одной из половин сосуда, невозможен.

Из сказанного выше следует, что для того чтобы определить, какие процессы могут протекать в изолированной системе, нужно знать вероятность различных состояний этой системы. Величина, характеризующая вероятность состояний, получила название энтропии.

Энтропия – функция состояния системы, изменение которой характеризует направление протекания самопроизвольных процессов. Функцией состояния называется такая физическая характеристика системы, изменение которой при переходе системы из одного состояния в другое не зависит от вида соответствующего этому переходу термодинамического процесса, а целиком определяется значениями параметров начального и конечного состояний.

Как всякая функция состояния, энтропия определяется только параметрами состояния и не зависит от процесса, с помощью которого система пришла в это состояние:

S = S(T,V),

S = S(P,V),                                       (2)           

S = S(T,P).

Бесконечно малое изменение энтропии системы определяется формулой:

                                                                                         (3)

где dQ – бесконечно малое количество тепла, сообщаемое системе при бесконечно малом изменении ее состояния; Т – абсолютная температура, при которой тепло поглощается системой. Отметим то обстоятельство, что dQ не является полным дифференциалом и не является изменением количества тепла.

Если система переходит из состояния 1 в состояние 2, то изменение энтропии равно:

                                          ,                                (4)

где S₁, S₂ – энтропия начального и конечного состояния системы.

При обратимом процессе, если система приходит в первоначальное состояние, то изменение энтропии равно нулю:

                                              ∮                                 (5)

т.е. энтропия изолированной системы при обратимом процессе остается постоянной (S =const).

Если система совершает необратимый процесс, то изменение энтропии определяется неравенством

                                                          .                                    (6)

Причем, из (6) следует, что если система изолирована, то

                                                                                              (7)

Неравенство (7), называемое неравенством Клаузиуса, утверждает следующее: «В изолированной системе, где протекают необратимые процессы, энтропия системы всегда возрастает» (закон возрастания энтропии). Объединяя соотношения (5) и (7), можно записать:

                                                                                              (8)

Соотношение (8) выражает математическую формулировку второго закона термодинамики: «Энтропия изолированной системы либо возрастает (при необратимом процессе), либо остается постоянной (при обратимом процессе)».

Таким образом, изменение энтропии характеризует направление протекания естественных процессов в замкнутой системе: естественные процессы проходят в направлении роста энтропии.

Опыт показывает, что замкнутая система, предоставленная самой себе, через некоторое время переходит в равновесное состояние, из которого без внешних воздействий не может выйти. В таких самопроизвольных процессах, как расширение газа, смешение двух газов и т.д., увеличение энтропии сопровождается увеличением степени неупорядоченности системы.

Л.Больцман (1896 г.) ответил на вопрос о физическом смысле энтропии. Согласно Больцману: энтропия – мера беспорядка в системе. Полный порядок соответствует минимуму энтропии, беспорядок - максимуму энтропии.

Больцман ввел понятие термодинамической вероятности W. Термодинамическая вероятность – это  число способов, с помощью которых можно осуществить данное состояние макросистемы, или число микросостояний, осуществляющих данное макросостояние. Макросостояние характеризуется термодинамическими параметрами системы P, V, T, m и др., которые характеризуют систему в целом. Микросостояния - различные способы размещения частиц, из которых состоит система.

Энтропия и термодинамическая вероятность связаны функцией:

                                                                                         (9)

где k – постоянная Больцмана.

Связь энтропии и термодинамической вероятности позволяет вскрыть статистический смысл второго закона термодинамики: всякий процесс в природе протекает в сторону увеличения вероятности состояния системы.

Например, разделенные газы до смешения можно считать более упорядоченными (менее вероятными), чем смешанные газы (неупорядоченные). Второе состояние более вероятное.

При изучении термодинамических процессов и некоторых общих вопросов термодинамики широко используется TS-диаграмма, в которой по осям абсцисс и ординат отложены соответственно энтропия и температура рассматриваемого тела.

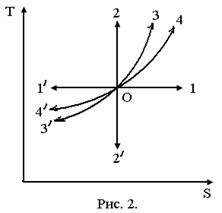
На рисунке 2 приведена TS-диаграмма для идеального газа. Пусть точка О на TS-диаграмме изображает начальное состояние идеального газа. Прямая 1^/-1, проходящая через точку О параллельно оси абсцисс, соответствует изотермическому процессу: 0 ®1 - изотермическое расширение (теплота подводится, так что dS > 0), 0 ®1^/ - изотермическое сжатие (теплота отводится - dS < 0). Прямая 2^/-2 изображает адиабатный (изоэнтропийный S = const) процесс: 0 ®2 - адиабатное сжатие (dT > 0) и 0 ®2^/ - адиабатное расширение (dT < 0). Кривая 3^/-3 изображает изохорный процесс: 0 ®3 - изохорное нагревание (dS > 0 и dT > 0), 0 ®3^/ - изохорное охлаждение (dS < 0 и dT < 0). Для изобарного процесса соответствует кривая 4^/-4: 0 ®4 - изобарное  расширение (dS > 0 и dT > 0), 0 ®4^/ - изобарное сжатие (dS < 0 и dT < 0).

Прямой цикл Карно изображается на TS-диаграмме в виде прямоугольника (рис. 3). Участок 1 ®2 соответствует изотермическому расширению (dS > 0), где подводится теплота, а участок 3 ®4 - изотермическое сжатие, при котором отводится теплота (dS < 0). Участок 2 ®3 соответствует адиабатному расширению (dT < 0 и S = const – изоэнтропийный процесс), 4 ®1 – адиабатное сжатие (dT > 0 и S = const).

1.      ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА

ИЗМЕРЕНИЙ

В работе используется система, состоящая из калориметрического стакана с водой и металлического тела.

На электроплитку (1) помещают стакан с водой (2), которую доводят до кипения. В кипящую воду опускается исследуемое тело (3). Через 3–5 мин оно нагревается до температуры Т₁. Измерение температуры воды в стакане производится с помощью термометра (4) (см. рис. 4).

Нагретое до температуры Т₁ тело (3) с помощью нитки, прикрепленной к нему, быстро вносится в калориметрический стакан (5) с водой при комнатной температуре Т₂ и закрывается крышкой (6). После того, как тело внесено в калориметр, систему «калориметр – тело – вода» можно считать изолированной, и пока температуры тела, калориметра и воды не выровняются, система находится в неравновесном состоянии. Через некоторое время она приходит в равновесное состояние.

Обозначим через Т₀ температуру всех тел системы в равновесном состоянии. При этом тело (3) охлаждается до температуры Т₀, отдавая некоторое количество теплоты системе «вода - калориметрический стакан», которые нагреваются до некоторой температуры Т₀.

Элементарное количество теплоты, отданное системе «вода - калориметрический стакан» нагретым телом (3) определяется соотношением:

                                                                               (10)

где   масса тела,  удельная теплоемкость тела.

Изменение энтропии тела  вычисляется по формуле:

                                        (11)

где  и  начальная и конечная температуры тела.

Элементарное количество теплоты, полученное водой и калориметрическим стаканом, равно:

                                                                                (12)

и

                                                                                  (13)

где   массы воды и калориметрического стакана, соответственно;  их удельные теплоемкости.

Изменения энтропии воды  и калориметрического стакана  рассчитываются по формулам:

                                                             (14)

                                                            (15)

где  начальная и конечная температуры воды и калориметрического стакана.

            Тогда общее изменение энтропии  всей системы «тело – вода – калориметрический стакан» равно:

    (16)

Измерив температуры Т₁, Т₂ и Т₀ и, зная массы и теплоемкости всех частей системы, можно определить изменение энтропии системы при ее переходе от неравновесного состояния к равновесному. В данной работе не учтена потеря количества тепла при переносе нагретых тел из стакана с кипящей водой (2) в калориметрический стакан (5), а также теплообмен с окружающей средой, которые существенно влияют на результаты эксперимента.

3.      ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА

РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1.   Включите электроплитку (1) и  поставьте на нее стакан (2) с водой.

2. Опустите за нитку в стакан с водой металлическое тело (3).

3.  Воду в стакане (2) нужно довести до кипения и измерить температуру Т₁ кипящей воды с помощью термометра (4).

4.  Пока вода вместе с исследуемым телом (3) нагреваются, отмерьте с помощью мерного стакана 150 мл холодной воды, налейте ее  в калориметрический стакан (5) и поставьте его подальше от плитки.

5.   Измерьте температуру Т₂ холодной воды в калориметрическом стакане с помощью термометра. При этом температура калориметрического стакана (5) равна температуре воды.

6.   Запишите в таблицу 1 массу металлического тела m_T, массу холодной воды m_В, массу калориметрического стакана m_К и температуры Т₁ и Т₂.

Значения масс исследуемых тел и калориметрического стакана возьмите у преподавателя или у лаборанта.

Таблица 1.

7.   За нитку вытащите тело из кипящей воды, быстро опустите его в калориметр (5) с холодной водой и закройте крышкой (6).

8.      Поместите в калориметр термометр и следите за ростом температуры. Запишите в таблицу максимальное значение температуры Т₀ всей системы «тело – вода – калориметрический стакан».

9.      Меняя воду в калориметре, проведите измерения по п.п. 2–8 для трех различных металлических тел, удельные теплоемкости которых приведены в таблице 2.

10. По формуле (16) рассчитайте изменение энтропии системы  для всех трех случаев и результаты вычислений занесите в таблицу 1.

Таблица 2.

4.      ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

1.  Сформулируйте цель работы.

2.  Опишите рабочую установку и ход эксперимента.

3.  Какие допущения делаете, рассматривая систему «тело – вода - калориметрический стакан» как изолированную?

4.  Напишите рабочую формулу, приведенную в данной работе.

5.  Какие законы используются для получения расчетной формулы?

6.  Какие состояния и процессы называются равновесными?

7.  Что называется изолированной термодинамической системой?

8.  Напишите формулу для вычисления абсолютной и относительной погрешности измерения  DS.

5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.      Сформулируйте первый закон термодинамики.

2.      Дайте определение обратимых и необратимых процессов. При каких условиях процессы будут обратимыми?

3.      Сформулируйте второй закон термодинамики и поясните его физический смысл. Чем он дополняет первый закон термодинамики?

4.      Опишите энтропию системы и ее физический смысл.

5.      Как вычисляется изменение энтропии при переходе ее из одного состояния в другое?

6.      Сформулируйте и напишите второй закон термодинамики, используя понятие энтропии.

7.      Статистический смысл энтропии.

8.      Какой знак имеет изменение энтропии для рассматриваемой в работе системы тел и почему?

9.       Поясните принцип действия тепловой машины.

10.  В чем сущность неравенства Клаузиуса?