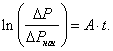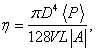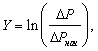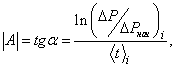|
Лабораторная работа № 205 ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ВОЗДУХА Цель работы: определить коэффициент
вязкости воздуха по истечению через капилляр. Приборы и принадлежности: капилляр, манометр, груша,
баллон, зажим,
соединительные шланги, секундомер. 1.
ВЯЗКОСТЬ (ВНУТРЕННЕЕ
ТРЕНИЕ) В ГАЗАХ При движении
соприкасающихся слоев газа (жидкости) друг относительно друга между ними
действуют силы внутреннего трения, или силы вязкости. Примером такого
движения может являться течение газа (жидкости) внутри трубки или капилляра.
Наличие сил вязкости приводит к тому, что скорость течения U зависит от расстояния до
оси трубки r (см. рис. 1), где
скорость течения условно обозначена стрелками. Она равна нулю непосредственно
вблизи стенок трубки (U(rо) = 0), а на ее оси (r = 0) достигает максимального значения. Возникновение
сил вязкости в газе связано с тем, что его молекулы участвуют одновременно в
двух движениях: упорядоченном и хаотическом тепловом. В нашем примере
упорядоченное или макроскопическое движение газа – это его течение по трубке.
Кроме этого молекулы газа движутся хаотически, причем среднее значение модуля
скорости теплового хаотического движения молекул обычно значительно превышает
скорость U упорядоченного движения.
Рис. 1. Выделим условно слой
газа, движущийся вдоль трубки круглого сечения с некоторым определенным
значением U. Этот слой представляет
собой полый цилиндр с внутренним радиусом r и внешним
r+dr и обозначен на рис. 1 пунктиром. В этот слой в результате теплового
движения попадают молекулы из соседних слоев. Из внешнего слоя с бóльшим
значением r в выделенный слой
попадают молекулы с меньшей скоростью, и, наоборот – из внутреннего слоя
попадают молекулы с бóльшей скоростью.
Происходит передача импульса
упорядоченного движения молекул в процессе их теплового движения. Внутренний
слой ускоряет, а внешний тормозит течение газа в выделенной области, что и
является проявлением сил внутреннего трения или вязкости. Тонкий слой газа,
непосредственно примыкающий к стенкам трубки, обволакивает ее и замедляет
движение соседнего слоя, который в свою очередь оказывает влияние на
следующий слой и т.д. Таким
образом, из вышесказанного следует, что существует две основные причины существования сил внутреннего трения при
движении слоев газа или жидкости относительно друг друга: 1) хаотическое тепловое движение молекул; 2) передача импульса при упорядоченном
движении молекул. Величина силы вязкости F, как следует из опыта,
прямо пропорциональна площади соприкасающихся слоев газа (жидкости) S и градиенту скорости их
движения по перпендикулярному ей направлению
r, т.е. производной где h - коэффициент вязкости или просто вязкость.
Модуль градиента скорости Для газов h зависит от температуры Таблица 1.
2. ПРИНЦИП ЭКСПЕРИМЕНТА И ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ Воздух накачивается в
сосуд до давления, превышающего атмосферное на некоторую величину
При проведении
эксперимента воздух вытекает из сосуда объемом V через капилляр длины L и диаметра D в атмосферу. Запишем уравнение состояния для
воздуха в этом сосуде: где m - молярная масса воздуха, m - масса воздуха в сосуде.
При проведении эксперимента можно считать температуру воздуха в сосуде
практически постоянной, тогда переменными величинами в уравнении (2) будут
только давление Р и масса m воздуха в сосуде. Поделив уравнение (2) на V и продифференцировав его
по времени, получим:
Расход воздуха
где r - плотность
воздуха, h - коэффициент вязкости, DР = Р - Ро - разность давлений на
концах капилляра, DL = L - длина капилляра, ro - его радиус. Знак «минус»
в соотношении (3) показывает, что с течением времени количество воздуха в
сосуде уменьшается. При небольших по сравнению с атмосферным давлением
значениях DР плотность воздуха r =
m/V можно считать постоянной
и выразить ее из уравнения состояния: где
где вместо производной или
где постоянная А дается выражением:
Интегрируя левую часть
уравнения (7) в пределах от
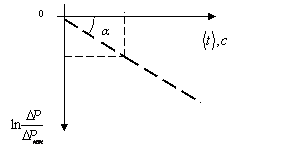
Введем обозначения: Тангенс А угла наклона прямой
позволяет определить значение коэффициента
вязкости h по формуле:
где Отметим, что полученное
соотношение (9) справедливо только для ламинарного течения воздуха вдоль
трубки. Ламинарным называется такое
течение, когда молекулы газа
(жидкости) движутся вдоль прямолинейных траекторий, параллельных оси трубки.
При больших скоростях ламинарное течение становится неустойчивым и переходит
в так называемое турбулентное течение. Турбулентное
течение – это такое течение, гидродинамические характеристики которого (для
газов – плотность и температура, а для жидкостей – скорость и давление)
быстро и нерегулярно изменяются во времени (флуктуируют). Молекулы газа
(жидкости) совершают нерегулярные, неустановившиеся движения по сложным
траекториям, это приводит к интенсивному перемешиванию слоев газа (жидкости).
Количественно характер
движения слоев газа (жидкости) определяется безразмерной величиной Re,
называемой числом Рейнольдса:
где
а это и есть число Рейнольдса.
Число Рейнольдса,
таким образом, определяет относительную
роль инерции и вязкости газа (жидкости) при течении. При больших числах Рейнольдса основную роль играет инерция, при малых –
вязкость. В нашем случае при небольшой (по сравнению с атмосферным)
разности давлений 3. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ На рис. 2 схематично
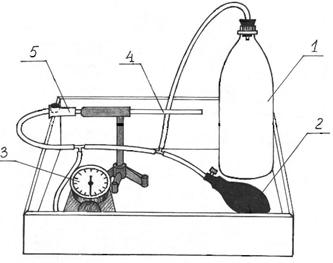
изображена экспериментальная установка для определения вязкости воздуха. Силиконовыми трубками при помощи двух тройников соединены между
собой баллон 1, резиновая груша 2, манометр 3 и закрепленный на
штативе капилляр 4, который перекрывается с помощью зажима 5. 1. Ознакомиться с работой секундомера (см. на корпусе установки). Если в вашем мобильном телефоне
есть секундомер с памятью, то можете использовать его при выполнении работы. 2. Перекрыть капилляр 4 зажимом 5 (кольцо
зажима перемещают в сторону капилляра до упора) и с помощью груши 2 накачать в баллон 1 воздух до разности давлений 3. Подождать несколько секунд, пока стрелка
манометра 3 не остановится. 4.
Открыть капилляр, ослабив зажим 5,
снять зависимость давления в баллоне от времени. Для этого при подходе
давления к выбранному значению Внимание! Значения времени этапов удобнее заносить
в таблицу снизу вверх, т.е. от последнего этапа к первому. 5. Стирание занесенных в
память «промежуточных результатов» (этапов) осуществляется нажатием и
удержанием кнопки D
в течение не менее 3 секунд (пока
не обнулятся показания всех этапов). После этого нужно еще раз быстро нажать
на кнопку D. Таким образом осуществится полное «обнуление» секундомера и он
снова будет готов к работе. 6. Операции по пунктам 2 – 6
повторить не менее пяти раз, результаты измерений времени занести в таблицу.
Рис.
2. 7. Рассчитать среднее
арифметическое значение времени
8. Рассчитать логарифмы
отношений 9. Среднее значение давления
где
атмосферное давление 10. Для определения углового коэффициента А (тангенса
наклона прямой
Рис. 3. Для расчета коэффициента А можно взять любую экспериментальную
точку, которая лежит на прямой:
где i – номер опыта или номер
экспериментальной точки. 11. По
формуле (9) рассчитайте вязкость воздуха h. Диаметр D и длина L капилляра, а также объем
V баллона указаны на
корпусе экспериментальной установки. 12. Сравните полученный
результат с табличным (см. в табл. 1 значение
вязкости воздуха при соответствующей температуре): и оцените относительную погрешность измерений в
процентах: Таблица 2. L = …м; D = …м; V
= … м3 ; Ратм
= … мм рт.ст.; t
= …°C.
4. ВОПРОСЫ
ДЛЯ ДОПУСКА К РАБОТЕ
2.
Поясните принцип эксперимента и ход работы. 3.
Запишите рабочую формулу для определения коэффициента вязкости воздуха
и поясните все величины, входящие в эту формулу. 5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 1. Объясните
молекулярно-кинетический механизм внутреннего трения. 2. Объясните
формулу (1), выражающую величину силы внутреннего трения. Что такое градиент
скорости? 3. Какие
существуют виды течения молекул газа (жидкостей) по капиллярным трубкам? При
каком течении справедлива формула Пуазейля? 4.
Что показывает число Рейнольдса? Каков его
физический смысл? 5. Выведите
расчетную формулу (9) для коэффициента динамической вязкости воздуха. 6. Покажите,
используя формулу (9), в каких единицах системы СИ измеряется коэффициент
динамической вязкости. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

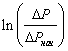 от
от