Лабораторная работа № 118

Определение скорости звука в воздухе методом резонанса

 Цель работы: Ознакомление с резонансным методом определения скорости звука.

Приборы и принадлежности: металлическая трубка с подвижным поршнем, звуковой генератор, измерительная линейка, электронный осциллограф, микрофон.

Теоретическое введение

 Как известно из курса физики, колеблющееся тело (камертон, струна, мембрана), находящееся в упругой среде, приводит в колебательное движение соприкасающиеся с ним частицы среды: атомы, молекулы и другие механические возмущения, возникающие в упругой среде. Вследствие чего в прилегающих к этому телу элементах среды возникают периодические деформации (например, растяжения или сжатия среды) и ведут к возникновению упругих сил, которые стремятся вернуть элементы среды в первоначальное состояние равновесия, то есть возникают упругие колебания среды.

Так как соседние элементы среды взаимодействуют друг с другом, то эти упругие деформации будут передаваться от одних участков среды к другим. Процесс распространения колебательного движения в среде называется механическими волнами. Волны могут быть продольными, когда частицы среды колеблются вдоль линии, совпадающей с направлением распространения колебания; и поперечными, когда частицы колеблются перпендикулярно к направлению распространения волны. В жидкостях и газах возникают только продольные волны, распространяющиеся в виде чередующихся сжатий и растяжений среды.

 Поверхность, до которой доходит колебание в некоторый момент времени, называется фронтом волны. Поверхность волны, в которой все частицы колеблются в одинаковой фазе, называется волновой поверхностью.

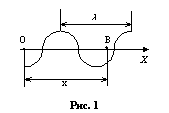
Для изотропной среды волновой фронт и волновая поверхность совпадают. Если частица упругой среды в точке О совершает колебательное движение по закону (рис.1)

где x (х,t) – смещение частицы среды от положения равновесия;
А – амплитуда (наибольшее смещение частицы среды от положения равновесия); t – время; Т – период; w = 2p/Т – циклическая или круговая частота; j₀ – начальная фаза колебания; то в соседнюю точку В среды придет колебательное движение с некоторым запаздыванием на время

,

где х – расстояние, на которое распространилось колебание от точки О до В. υ – скорость распространения волны (фазовая скорость волны).

 Уравнение смещений частицы среды в точке В запишется

при условии j₀ = 0.

Это общее уравнение бегущей плоской синусоидальной волны. Оно определяет для любого момента времени t отклонение от положения равновесия колеблющихся частиц, находившихся в покое на расстоянии х от начала отсчета. Расстояние l, пройденное волной (определенной фазой колебания) за один период колебания, называется длиной волны, т.е. длина волны – кратчайшее расстояние между соседними частицами среды, колеблющимися в одинаковой фазе.

где n - частота колебания частиц среды.

 Частоты колебаний n частиц среды имеют ту же частоту, что и частота колебаний источника волн. Волны, частоты колебаний частиц в которых лежат в пределах от 16 до 20000 Гц, называются звуковыми.

 Звуковые волны в газах и жидкостях являются продольными и могут распространяться только в упругой среде.

 Звуковые волны, как и электромагнитные, обладают рядом свойств: интерференцией, дифракцией, отражением и т.д.

 Интерференцией волн называется явление усиления или ослабления колебаний, которые происходят в результате наложения двух или нескольких когерентных волн. Когерентными называются волны, распространяющиеся в среде с одинаковой частотой и с постоянной по времени разности фаз. Частным случаем интерференции волн являются стоячие волны, которые образуются при наложении двух встречных волн с одинаковой амплитудой и частотой. Практически стоячие волны возникают при отражении волн от преграды.

 Предположим, что две плоские волны с одинаковыми амплитудами и частотами распространяются вдоль оси Х в противоположных направлениях. Если начало координат взять в такой точке, в которой встречные волны имеют одинаковую фазу, и выбрать отсчет времени так, чтобы начальные фазы оказались равными нулю, то уравнение обеих плоских волн можно написать в следующем виде. Для волны, идущей в сторону положительной оси Х

и для волны, идущей в сторону отрицательной оси Х

Сложение этих двух волн дает

или, раскрывая значения косинусов от сложных аргументов и производя сокращения, получим уравнение стоячей волны

Множитель 2А×cos2pх/l, не зависящий от времени t, выражает амплитуду В стоячей волны, т.е.

 Таким образом, амплитуда стоячей волны зависит от координаты x, определяющей положение колеблющей частицы.

 В точках, координаты которых удовлетворяют условию

,

амплитуда стоячей волны достигает максимального значения. Эти точки называются пучностями стоячей волны.

 В точках, координаты которых удовлетворяют условию

амплитуда стоячей волны обращается в нуль. Эти точки называются узлами стоячей волны.

 Расстояние между соседними узлами или пучностями называется длиной стоячей волны (l_ст). Длина звуковой (бегущей) волны - l = 2l_ст.

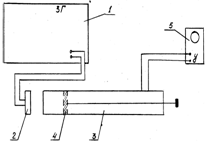
Описание рабочей установки и метода измерений

 В экспериментальной установке (рис.2), состоящей из звукового генератора 1 с телефоном 2, трубки 3 (в которой образуются стоячие волны) и подвижного поршня 4, звуковые волны распространяются только вдоль трубки. Звуковые волны преобразуются в электрический сигнал и подаются на вертикальный вход электронного осциллографа 5.

 Звуковые стоячие волны образуются: 1) из прямой волны (сплошная линия), идущей от телефона 2 к поршню 4 (рис.3); 2) из отраженной (пунктир) от поршня 4 волны, фаза которой изменилась на p, так как отражение происходит от среды акустически более плотной. В данном случае при отражении произошла потеря полуволны. При определенных условиях в трубке 3 возникает акустический резонанс.

 Резонанс – это явление резкого возрастания амплитуды вынужденных колебаний в колебательной системе при приближении частоты внешней силы (вызывающей вынужденные колебания) к частоте какой-либо из собственных колебаний данной колебательной системы. В данном случае имеем акустический резонанс, т.е. явление, при котором колебания столба воздуха в трубке достигают максимальной амплитуды. Это происходит тогда, когда частота звуковых колебаний мембраны (внешняя, вынуждающая сила) приближается к одной из собственных частот воздушного столба в трубке. Это частота называется резонансной частотой. При резонансной частоте звучание воздушного столба в трубке максимально.

 Для наблюдения акустического резонанса нужно, чтобы столб воздуха в трубке 3 между поршнем 4 и открытым концом резонировал на звуковые волны, возбуждаемые источником звука – телефоном 2. Для этого необходимо, чтобы длина l столба воздуха в трубке между открытым концом и поршнем 4 удовлетворяла условию

,

где m = 1, 2, 3…

 На рис.4 на длине l столба воздуха в трубке укладывается пять половин стоячей волны (при m = 3).

 В работе находят расстояние d l между двумя ближайшими положениями поршня – двумя соседними пучностями, соответствующими наибольшей громкости звука. На рис.4 показано положение поршня в двух узлах, например, 1 и 2. Так как длина стоячей звуковой волны l_ст = d l, то длина искомой звуковой волны

Рис. 4

Если постепенно отодвигать поршень от телефона, то можно добиться резонанса, т.е. максимального звучания воздушного столба, заключенного в трубке, и в трубке будет слышно последовательно усиление или ослабление звука. В трубке образуются стоячие волны, причем у поршня всегда будет узел, а у открытого конца – пучность. Зная длину звуковой волны l и частоту n, которая указана на звуковом генераторе, определяют фазовую скорость распространения звуковой волны в воздухе по формуле

                                      (7)

Ход работы

Излучателем звуковых волн в работе служит телефон ДЭМШ-1. На телефон подается переменное напряжение звуковой частоты от низкочастотного генератора ГЗ-102. Звуковые колебания воздуха преобразуются микрофоном МД-201 в электрический сигнал, подаваемый на вертикальный вход электронного осциллографа ЛО-70 (рис.2).

Для получения звукового сигнала надо (только с разрешения преподавателя или лаборанта) включить генератор ГЗ-102 в сеть, затем поставить тумблер СЕТЬ в положение «вкл» – при этом загорается сигнальная лампочка. Предварительно следует установить ручки на панели генератора: «множитель частот» – в положение 10, «регулировка напряжения» – в крайнее левое положение 50.

Дают генератору погреться 15 минут, затем ручкой настройки устанавливают выходную частоту генератора 1500 Гц, ручкой «регулировка напряжения» стрелку вольтметра на панели прибора устанавливают в положение между делениями 5-6 на верхней шкале.

Включают в сеть осциллограф. Переключатель «диапазон частот» на панели осциллографа устанавливается в положение 2, ручка СИНХ – среднее положение. С помощью ручки «частота плавно» получают устойчивое изображение сигнала на экране. Затем приступают к измерениям.

Медленно и равномерно отодвигается поршень от телефона по шкале, нанесенной на штоке, последовательно отмечают и записывают положения l_i, при которых сигнал на экране осциллографа максимально усиливается.

Вычисляется расстояние d l = l_i+1 – l_i. Следует найти не менее пяти значений d l.

1.      По формуле (6) вычисляют длину звуковой волны для каждого из опытов, а по формуле (7) вычисляют фазовую скорость распространения звука (также для каждого опыта).

2.      Находят среднюю скорость звука и подсчитывают абсолютную и относительную погрешности результата, исходя из среднего значения искомой величины.

3.      Измерения повторяют при частоте 2000 Гц.

4.      Результаты измерений и вычислений заносят в таблицу.

Таблица

Вопросы для допуска к работе

1.        Какова цель работы?

2.        Опишите метод нахождения длины звуковой волны в работе.

3.        Запишите формулу для определения скорости звука в работе.

4.        Оцените погрешность метода измерений скорости звука в работе.

Вопросы для защиты работы

1.      Что называется механической волной? Какая волна является продольной? Поперечной?

2.      Получите уравнение плоской бегущей волны.

3.      Что называется интерференцией волн?

4.      Выведите уравнение стоячей волны.

5.      Что такое пучность, узел стоячей волны?

6.      Какими свойствами обладают механические волны?

7.      Что называется звуком?

8.      От чего зависит скорость распространения звуковой волны в твердых, жидких, газообразных веществах? Выведите ее.

9.      Выведите энергию и интенсивность бегущей волны.

10.  Что называется высотой звука? От чего зависит громкость звука?

11.  Что называется инфразвуком, ультразвуком? Расскажите об их применении.