Лабораторная работа № 116

Определение коэффициента упругости

Цель работы: Экспериментальное определение коэффициента упругости стальной пружины методом колебаний.

Приборы и принадлежности: пружинный маятник, секундомер, грузы, технические весы.

Теоретическое введение

 Под действием приложенных к нему сил всякое реальное тело деформируется, т.е. изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, если сила, обусловившая деформацию, не превосходит некоторый, определенный для каждого тела, предел.

 Опыт показывает, что при упругой деформации для тела выполняется закон Гука, который гласит: упругая сила пропорциональна абсолютному удлинению тела, т.е.

,

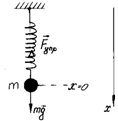
где k – коэффициент упругости тела; Dl – абсолютное удлинение.

Рассмотрим пружинный маятник, представляющий собой упругую пружину с коэффициентом упругости k, на одном конце которой подвешено тело массой m, а другой конец закреплен (рис.1).

В свободном состоянии маятника на тело массой m действуют сила тяжести  и упругая сила , которые равны по величине и противоположны по направлению. Поэтому тело массой m будет находиться в состоянии покоя (равновесия) (рис.1). Приложим к телу массой m внешнюю силу , которая сместит тело из положения равновесия вниз на расстояние х (рис.2), затем уберем эту силу и предоставим маятник самому себе. Под действием упругой силы тело возвращается в положение равновесия, по достижению его тело по инерции будет двигаться вверх, сжимая пружину. При сжатии пружины возникает упругая сила, направленная вниз по оси х, которая разжимает пружину. При этом тело будет двигаться вниз и, пройдя положение равновесия, по инерции опустится вниз по оси х. При этом в пружине возникает упругая сила, направленная вверх, которая заставляет подниматься тело вверх. При отсутствии диссипативных сил (в частности, силы сопротивления) и при выполнении закона Гука F_упр= -kх, тело будет совершать гармонические колебания.

Найдем уравнение колебания пружинного маятника и период колебания.  Для этого используем закон сохранения механической энергии. В любой момент времени полная механическая энергия пружинного маятника остается постоянной, если отсутствуют диссипативные силы и система изолирована. Тогда сумма кинетической энергии  и потенциальной энергии - постоянна

где υ – скорость тела, х – смещение тела от положения равновесия, причем

.

Продифференцировав (1) по времени, получим

,

Откуда

.

Обозначив

,

получим

Соотношение (3) является дифференциальным уравнением гармонического колебания пружинного маятника, совершающегося с циклической частотой w. Циклическая частота равна числу полных колебаний, совершаемых за время 2p с.

Решением дифференциального уравнения (3) служит уравнение гармонического колебания

где х – смещение колеблющегося тела от положения равновесия в момент времени t; А – амплитуда колебания, равная наибольшему смещению тела от положения равновесия;  j₀ – начальная фаза колебания.

 Период колебания, равный времени, за которое совершается одно полное колебание, определяется формулой

Период колебания пружинного маятника зависит от коэффициента упругости пружины и массы колеблющегося тела.

 Из формулы (5) коэффициент упругости пружины равен

Описание рабочей установки и метода измерений

 Рабочая установка представляет собой пружинный маятник (рис.3), состоящий из груза Г, подвешенного к пружине б. Пружина крепится к перекладине, закрепленной на двух штативах а.

 Если груз вывести из состояния покоя, то под действием упругой силы пружины он начнет совершать гармонические колебания. Зная массу груза m и период колебаний Т, по формуле (6) легко находится коэффициент упругости пружины k.

 Правильность найденного значения коэффициента упругости k проверяется по формуле, являющейся выражением закона Гука:

где P = mg – вес груза, под действием которого пружина удлиняется на величину Dl. Значение Dl отсчитывают по смещению миллиметровой линейки в, укрепленной с пружиной относительно указателя смещения g.

Ход работы

1.      Подобрать массу груза так, чтобы можно было легко считать число колебаний маятника. Определить массу груза m взвешиванием на технических весах.

2.      Исходя из 30-50 полных колебаний, определить период колебаний груза

,

где <t> - среднее время n полных колебаний.

Время t измерить секундомером. С данным грузом время t измерить не менее 5 раз для одного и того же числа колебаний и определить среднее значение времени <t>.

3.      По формуле (6) найти значение коэффициента упругости k.

4.      Грузы привести в статическое состояние, и, по смещению линейки относительно указателя, определить удлинение пружины Dl под действием веса груза.

5.      По формуле (7) найти среднее значение k_пров.

6.      Опыт повторить при другой массе груза.

7.      Вычислить абсолютную и относительную погрешности коэффициента упругости k.

8.      Данные занести в таблицу.

Таблица

Вопросы для допуска к работе

1.      Какова цель работы?

2.      Запишите рабочую формулу и поясните величины, входящие в нее.

3.      Опишите рабочую установку и ход эксперимента.

4.      Оцените погрешность метода измерений коэффициента упругости.

Вопросы для защиты работы

1.      Опишите колебания пружинного маятника.

2.      Выведите дифференциальное уравнение гармонического колебания для пружинного маятника.

3.      Напишите уравнение гармонического колебания пружинного маятника и поясните физический смысл всех величин.

4.      Дайте определение циклической частоты и периода колебания.

5.      От чего зависят циклическая частота и период колебания пружинного маятника?

6.      Выведите рабочую формулу.

7.      Каков физический смысл коэффициента упругости?

8.      Какие колебания называются свободными? Вынужденными?

9.      Вычислите погрешность результата эксперимента, пользуясь дифференцированным методом.