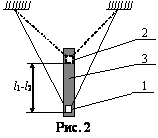Лабораторная работа № 111

Математический маятник

Цель работы: Экспериментальное определение ускорения силы тяжести методом колебаний математического маятника.

Приборы и принадлежности: математический маятник, секундомер, зеркальная шкала.

Теоретическое введение

Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой и длинной  нити. На практике математическим маятником можно считать тяжелое тело, подвешенное на нити, длина которой во много раз больше размеров тела. Длиной l математического маятника называется расстояние от центра масс тела до точки подвеса нити.

Если отклонить маятник из положения равновесия так, чтобы нить составляла небольшой угол j с вертикалью (рис.1), и затем отпустить его, то он начнет колебаться в вертикальной плоскости под действием силы тяжести  и силы натяжения нити . Сила , возвращающая математический маятник в положение равновесия, является равнодействующей сил тяжести   и натяжения нити. Ее можно найти из рисунка 1:

Период и частоту колебания математического маятника можно найти из закона сохранения механической энергии.

В отсутствии сил сопротивления полная механическая энергия маятника в любой момент времени остается постоянной, т.е. сумма кинетической энергии  и потенциальной энергии маятника :

где h – высота подъема материальной точки от положения равновесия.

Из рис.1 найдем h. Она равна

Момент инерции J материальной точки определяется формулой:

Учитывая, что угловая скорость равна , а угловое ускорение равно, а так же (2) и (3), то выражение (1) можно записать в виде:

Взяв первую производную по времени, получим:

 или

где                                    

При малых углах j<6° выполняется условие, что  Тогда уравнение (4) можно записать в виде

(6) является однородным дифференциальным уравнением второго порядка, описывающим гармонические колебания маятника. Решение этого уравнения имеет вид:

где А, a₀ – амплитуда и начальная фаза колебания. Величина w в формуле (5) является циклической частотой колебания математического маятника.

Период колебаний маятника определяется формулой:

который зависит от длины l маятника и ускорения свободного падения g тел.

Описание рабочей установки и метода измерений

Периоды колебаний двух математических маятников с различными длинами l₁ и l₁ согласно формуле (8) равны:

Из этих двух равенств получим:

Откуда следует:

Формула (9) является исходной для определения величины ускорения свободного падения.

 В данной работе математическим маятником служит груз 1, подвешенный бифилярно на длинной легкой нити 2, таким образом, длину которой можно менять (рис.2). Бифилярная подвеска (на двойной нити) позволяет осуществлять колебания в одной плоскости. Величина изменения длины математического маятника l₁-l₂, входящая в формулу (9), измеряется с помощью зеркальной шкалы 3.

Ход работы

1.      Длину маятника подбирают так, чтобы груз 1 находился в нижней части шкалы 3. Отсчитывают положение нижней грани груза по шкале, располагая глаз так, чтобы эта грань и ее изображение в зеркале шкалы совпадали.

2.      По секундомеру определяют время t₁  50-70 полных колебаний. Опыт повторяют не менее 5 раз и находят среднее значение . Определяют период колебания:

где n – число колебаний маятника.

3.      Укорачивая нить, перемещают груз в верхнюю часть шкалы и отсчитывают положение нижней грани груза l₂. Разность отсчетов l₁-l₂ равна изменению длины маятника.

4.      Измеряют не менее 5 раз время t₂ того же числа колебаний n. Вычисляют период колебаний:

5.      По формуле (9) вычисляют значение <g>.

6.      Методом расчета погрешностей косвенных измерений находят абсолютную погрешность результата Dg.

7.      Данные результатов измерений и вычислений заносят в таблицу.

Таблица

Вопросы для допуска к работе

1.      Какова цель работы?

2.      Что называется математическим маятником?

3.      Запишите формулу периода колебаний математического маятника и поясните величины, входящие в нее. При каких условиях справедлива эта формула?

4.      Опишите рабочую установку и ход работы.

5.      Оцените погрешность метода измерения ускорения свободного падения.

Вопросы для защиты работы

1.      Под действием каких сил совершает гармонические колебания математический маятник?

2.      Исходя из закона сохранения механической энергии, получите дифференциальное уравнение гармонических колебаний математического маятника, приведите его решение.

3.      При каких условиях маятник будет совершать гармонические колебания?

4.      Выведите формулу периода колебаний математического маятника.

5.      Получите рабочую формулу для определения величины ускорения свободного падения.

6.      Получите дифференциальным методом формулу для расчета относительной погрешности Dg/g и укажите пути повышения точности результата эксперимента.