ЛАБОРАТОРНАЯ РАБОТА №105

Определение скорости пули при помощи баллистического

крутильного маятника

Цель работы: Определение скорости полета пули при помощи баллистического крутильного маятника.

Приборы и принадлежности: баллистический крутильный маятник FPM-09, пуля, измерительная линейка.

Теоретическое введение

Момент инерции является физической величиной, характеризующей распределение масс в теле, и являющийся мерой инертности тела (аналог массы) при вращательном движении. Моментом инерции материальной точки J_i относительно, какой-либо оси называется произведение ее массы т_i на квадрат расстояния до этой оси r_i

Для определения момента инерции твердого тела относительно некоторой оси разобьем его на п – малых элементов, каждый из которых можно принять за материальную точку. Момент инерции твердого тела относительно оси ОО^/ (рис.1) равен сумме моментов инерции всех точек относительно этой оси.

Момент инерции тела, имеющего плотность r, вычисляется по формуле

где dV– элемент объема.

Момент инерции относительно данной оси, как и масса тела, не зависит от характера движения, а зависит от размеров, формы и плотности тела.

Если момент инерции относительно оси вращения, проходящей через центр масс, равен J₀, то момент инерции тела J относительно любой другой оси, параллельной первой, может быть определен на основании теоремы Штейнера:

где m– масса тела, d– расстояние между осями.

Во вращательном движении аналогом импульса тела является момент импульса. Момент импульса L материальной точки массой m, движущейся по окружности радиусом r со скоростью υ равен:

Для определения момента импульса твердого тела, вращающегося с угловой скоростью w, выделим n- малых элементов, каждый из которых можно принять за материальную точку.

Момент импульса i-элемента равен:

т.к . то

Момент импульса твердого тела относительно оси вращения ОО^/ равен сумме моментов импульсов всех точек тела относительно этой оси:

т.е. момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость.

Основной закон динамики вращательного движения имеет вид

где М– величина суммарного момента внешних сил, действующих на тело; w – угловая скорость тела; J – момент инерции тела относительно оси вращения.

Если М = 0, то Jw =const. Таким образом, если момент сил, действующих на тело, равен нулю, то тело будет покоиться или вращаться бесконечно долго, сохраняя постоянным момент импульса. Это утверждение, в сущности, является одной из формулировок закона сохранения момента импульса

при

При вращении твердого тела относительно неподвижной оси отдельные элементы массой m_i опишут окружности различных радиусов r_i и будут иметь различные линейные скорости U_i, а угловая скорость вращения ω этих элементов одинакова.

Кинетическая энергия i- элемента равна:

т.к. то

Кинетическая энергия твердого тела относительно неподвижной оси вращения ОО^/ равна сумме кинетических энергий всех точек тела относительно этой оси

т.е. кинетическая энергия твердого тела относительно неподвижной оси вращения равна половине произведения момента инерции тела относительно этой оси на квадрат угловой скорости.

Описание рабочей установки и метода измерения

Подпись:
Рис. 2. Крутильный маятник
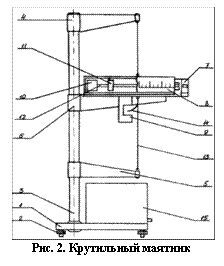
Крутильный баллистический маятник представляет собой массивное тело со значительным моментом инерции, подвешенное на упругой нити. Крутильный маятник FРМ-09 (рис.2) состоит из основания 1, оснащенного регулируемыми ножками 2, позволяющими установить прибор горизонтально. В основании закреплена колонка 3, на которой закреплены три кронштейна: верхний 4, нижний 5 и средний 6. К среднему кронштейну прикреплены: стреляющее устройство 7, прозрачный экран с нанесенной на нем угловой шкалой 8, фотоэлектрический датчик 9. К кронштейнам 4 и 6 при помощи зажимов крепится стальная проволока 13, на которой подвешен маятник, состоящий из двух мисочек, наполненных пластилином 10, двух подвижных грузов 11, двух стержней 12, водилки 14.

Подпись:
Рис. 3
Фотоэлектрический датчик 9 (рис.2), разъемом, соединен с универсальным миллисекундомером FРМ-14 (15 на рис.2), привинченным к основанию маятника. Универсальный миллисекундомер (рис.3) включает счетчик полных колебаний 2, счетчик времени полных колебаний 3, переключатели «СЕТЬ» 4, «СБРОС» 5, «СТОП» 6.

Для определения скорости полета пули используется крутильный баллистический маятник.

Пуля после выстрела застревает в пластилине, находящемся в одной из мисочек крутильного маятника, что вызывает отклонение маятника на некоторый угол.

Считая удар неупругим запишем закон сохранения момента импульса

где m– масса пули, υ– ее скорость, r– расстояние от оси вращения маятника до точки застревания пули в пластилине, -момент импульса тела, w – угловая скорость, J₁– момент инерции маятника.

Закон сохранения механической энергии (после удара) дает

где максимальная потенциальная энергия деформации кручения; a – наибольший угол поворота маятника; D – модуль кручения, -кинетическая энергия маятника при вращательном движении.

Выразив угловую скорость ω из уравнения (1) и подставив ее в (2), получим

Учитывая, что момент инерции пули относительно оси вращения много меньше момента инерции маятника относительно этой же оси (mr² << J₁), можно записать

Маятник после попадания пули совершает гармонические колебания. Уравнение движения маятника имеет вид:

где – угловое ускорение.

Решение уравнения (5) приводит к выражению для периода колебаний Т₁

Аналогично период колебаний для момента инерции J₂

(6а)

Для нахождения Т₁ и Т₂ каждый из грузов 11 устанавливают вначале на расстоянии R₁ от оси вращения, а затем на расстоянии R₂.

На основании формул (6) и (6а) можно записать

где J₁и J₂– моменты инерции маятника относительно оси, совпадающей с осью проволоки, при удалении от нее каждого подвижного груза 11 соответственно на R₁ и R₂.

Согласно теореме Штейнера:

где J₀– общий момент инерции всех тел системы относительно осей, проходящих через центр масс каждого тела; М – масса одного груза.

Найдя разность

с учетом (7), составим пропорцию

получим

Выразим J₁ из (6) и приравняем полученное выражение с (12), получим для модуля кручения

(13)

Подставив (12) и (13) в (4) запишем

Ход работы

1. Включить сетевой шнур измерителя в сеть, нажать клавишу «СЕТЬ», проверяя, все ли индикаторы измерителя высвечивают цифру ноль, светится ли лампочка фотоэлектрического датчика.

2. Пулю закрепить в стреляющем устройстве.

3. Расположить подвижные грузы (11) на минимальном расстоянии от оси вращения крутильного маятника. Измерить расстояние R₁ от оси вращения до центра подвижного груза.

4. Крутильный маятник установить на черте 0^° угловой шкалы.

5. Произвести выстрел, измеряя максимальный угол поворота маятника по угловой шкале a и расстояния от оси вращения маятника до точки застревания пули в пластилине r.

6. Отклонить рукой маятник на максимальный угол (a), нажать клавишу «СБРОС», одновременно пустив маятник, измерить время десяти полных колебаний, нажать клавишу «СТОП» в конце измерения; вычислить период колебаний Т₁, опыт повторяют 5 раз с одним и тем же числом колебаний.

7. Раздвинуть подвижные грузы на максимальное расстояние от оси вращения и измерить расстояние R₂ от оси вращения до центра подвижного груза, согласно пункту 6 определить период колебаний Т₂.

8. Вычислить скорость пули υ по формуле (14). Масса пули m = 2,03 г. Масса подвижного груза М = 200 г.

9. Методом расчета погрешностей косвенных измерений находят абсолютную погрешность Dυ

10. Данные результатов измерений заносят в таблицу.

Таблица результатов

№

M

R₁

t₁

<t₁>

T₁

R₂

t₂

<t₂>

T₂

υ

Dυ

E

кг

м/с

Вопросы для допуска к работе

1. Какова цель работы?

2. Опишите рабочую установку и ход эксперимента.

3. Запишите рабочую формулу для определения скорости полета пули.

4. На основе каких законов получена рабочая формула?

5. Оцените погрешность метода измерения скорости пули.

Вопросы для защиты работы

1. Какой удар называется абсолютно упругим, неупругим?

2. Что называется моментом силы, моментом импульса, моментом инерции материальной точки, твердого тела?

3. Сформулируйте основной закон динамики вращательного движения, закон сохранения момента импульса.

4. Сформулируйте теорему Штейнера.

5. Назовите виды механической энергии. Сформулируйте закон сохранения механической энергии?

6. Выведите рабочую формулу (14)?

7. Есть ли критические замечания к рабочей установке (как повысить точность результата эксперимента)? Какой еще эксперимент можно осуществить на данной установке?