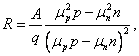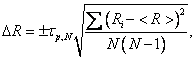Лабораторная работа № 405.

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ НОСИТЕЛЕЙ ТОКА В ПОЛУПРОВОДНИКЕ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА

Цель работы:   1) определение  постоянной Холла;

2) определение концентрации носителей заряда.

Приборы и принадлежности:  установка для изучения эффекта Холла, образец  (датчик Холла), источник питания образца, цифровые вольтметры.

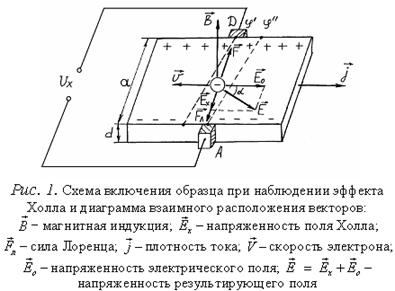
1.      ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

Более века тому назад (1879г.) американский физик Холл, поместив тонкую золотую пластинку в магнитное поле, обнаружил, что при протекании по ней электрического тока в направлении, поперечном вектору магнитной индукции и вектору плотности тока, появляется электрическое поле. Этот эффект впоследствии был назван эффектом Холла, а поперечное электрическое поле – полем Холла.

Эффект Холла непосредственно связан с подвижностью и концентрацией носителей заряда, а знак ЭДС Холла зависит от знака заряда. Поэтому эффект Холла широко применяется при исследовании электрических свойств различных материалов и для контроля качества полупроводниковых материалов, идущих на изготовление приборов.

Изучение температурной зависимости эффекта Холла дает важную информацию о механизмах рассеяния[1] носителей заряда, о ширине запрещенной зоны материала и энергии ионизации различных примесей.

Весьма широкое применение эффект Холла находит в современной технике, являясь основой для создания приборов различного назначения: магнитометров, преобразователей постоянного тока в переменный и переменного в постоянный, усилителей постоянного и переменного тока, микрофонов, приборов автоматики и контроля, элементов вычислительной техники и многого другого.

Эффект Холла является прямой демонстрацией действия силы Лоренца на движущиеся электрические заряды.

Рассмотрим проводник (или полупроводник) в виде параллелепипеда шириной а и толщиной d, через который протекает электрический ток плотностью, как показано на рис.1. Предположим также, что в проводнике имеются носители заряда одного знака: либо электроны, либо дырки. Проведем рассмотрение электронного проводника. Выберем на гранях, параллельных току, точки А и D, лежащие на одной эквипотенциальной поверхности[2] . Напряжение между этими точками U_x= 0.

Поместим проводник в магнитное поле, вектор индукции  которого перпендикулярен направлению тока и боковым граням. Под действием силы Лоренца

электроны отклоняются к передней (по рисунку) грани образца, заряжая ее отрицательно. На противоположной грани образца накапливаются нескомпенсированные положительные заряды. Это приводит к появлению электрического поля  

Смещение и разделение зарядов будет продолжаться до тех пор, пока сила Лоренца не уравновесится силой  действующей на электроны со стороны поля Холла

Сила, действующая на электрон в условиях динамического равновесия, равна

или

Отсюда поле Холла

Результирующее электрическое поле

повернется при этом на угол Холла a, определяемый выражением

относительно вектора  Соответственно эквипотенциальные поверхности  и  тоже изменят свое положение, и точки А и D в результате окажутся на разных эквипотенциальных поверхностях и между ними появится напряжение (ЭДС Холла):

Так как

и                      то есть         

то можно записать, что

и ЭДС Холла

где учтено, что

Величина  называется постоянной Холла. Знак постоянной Холла зависит от знака заряда и определяет направление поля Холла (рис.2). У электронных полупроводников (полупроводников n-типа) R имеет отрицательный знак, у дырочных (полупроводников р-типа) – положительный.

Таким образом, определяя постоянную Холла и ее знак, можно определить концентрацию и знак носителей тока в полупроводнике.

Рассмотренная модель эффекта Холла применима для проводников (металлов) и вырожденных полупроводников[3], т.е. к проводникам, в которых имеются носители одного знака, обладающие одинаковой скоростью  В невырожденных полупроводниках скорость носителей подчиняется распределению Максвелла. Учет этого обстоятельства приводит к формуле

где А – постоянная, зависящая от механизма рассеяния носителей.

В полупроводниках со смешанной проводимостью перенос тока осуществляется одновременно электронами и дырками. Так как они обладают противоположными по знаку зарядами и под действием внешнего поля перемещаются в противоположные стороны, то сила Лоренца  отклоняет их в одну и ту же сторону. Поэтому при прочих равных условиях ЭДС Холла и постоянная Холла у таких проводников меньше, чем у проводников с одним типом  носителей. Расчет показывает, что для таких проводников

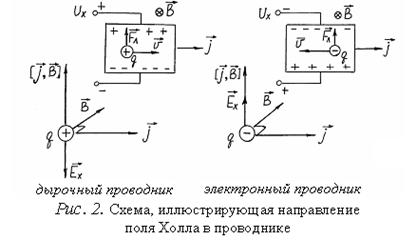
где n и р – концентрации электронов и дырок, m_n и m_р – их подвижности.

В зависимости от того, какое из слагаемых числителя больше, знак Холла может быть положительным или отрицательным. Для собственных полупроводников, у которых концентрации электронов и дырок одинаковы, знак постоянной Холла определяется знаком носителей, имеющих более высокую подвижность. Обычно такими носителями являются электроны. Поэтому в примесном дырочном полупроводнике (полупроводнике р-типа) при повышении температуры и переходе к собственной проводимости постоянная Холла проходит через нуль и меняет знак.

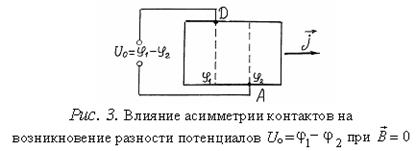
При измерении постоянной Холла и напряжения Холла следует иметь ввиду, что между холловскими электродами А и D имеется некоторая разность потенциалов U_о и в отсутствии магнитного поля  Эта разность потенциалов обусловлена асимметрией контактов (на практике очень трудно расположить их на одной эквипотенциальной поверхности, см. рис.3), и термоэдс, связанной с неизотермичностью образца. Для исключения влияния начальной разности потенциалов U_о на результаты измерения можно воспользоваться следующим методическим приемом.

При изменении направления магнитного поля на обратное знак ЭДС Холла U_х изменится, в то время как знак U_о остается прежним. При этом в зависимости от соотношения величин U_х и U_о возможны два подхода к определению U_х . Чаще встречается случай, когда  Тогда для различных направлений  (условно обозначенных ниже знаками + и - ) измеряемое напряжение U меняет свой знак, и можно записать:

Вычитая из первого уравнения второе, получим

                                                                              (1)

Если U_х < U_о , тогда при различных направлениях  знак измеряемого напряжения не изменяется и можно записать

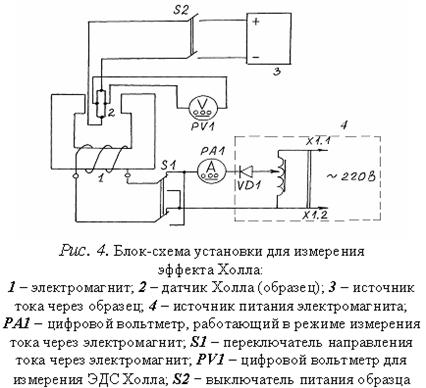
Вычитая из первого уравнения второе, получим

                                                                              (2)

2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ

Установка состоит из трех основных частей: 1) – электромагнит со схемой питания; 2) – схема питания датчика Холла; 3) – измерительная часть для определения знака и величины ЭДС Холла.

3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА

РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

1.      Включить источник питания электромагнита 4.

2.  Включить  источник  тока 3 через образец.  Ток, протекающий через образец   I = 35 мА.

3.  Провести измерения холловской разности потенциалов, меняя величину тока I_э, текущего через электромагнит с шагом примерно 0,02 А в интервале от 0,02 до 0,12 А. Величина тока электромагнита регулируется лабораторным автотрансформатором, включенным в цепь питания электромагнита и измеряется цифровым вольтметром РА1, работающим в режиме измерения силы тока.

Измерения холловской разности потенциалов при каждом установленном значении тока I, выполнять при двух направлениях тока (одному направлению соответствует значение напряжения , другому - ). Направление тока изменяется переключателем S1, установленным на лицевой панели прибора. Результаты измерений  и  занести в таблицу.

Таблица результатов

4.  По формуле (1) или (2) рассчитать ЭДС Холла U_х  для каждого значения тока электромагнита I_э. Если при смене направления тока  I_э  знак противоположен знаку , то следует пользоваться формулой (1), в противном случае – формулой (2).

5.  По графику зависимости индукции магнитного поля от тока в обмотке электромагнита, имеющегося на рабочем столе, или по формуле

где а и b – коэффициенты, определить величину индукции магнитного поля В.

6.  Определить значение постоянной Холла по формуле

где  d = 5,0×10^-5 м, I = 35,0×10^-3 A.

7.  Определить среднее значение постоянной Холла.

8. Рассчитать концентрацию носителей тока на основании соотношения

   где   е = 1,6×10^-19 Кл.

9.      Определить погрешность постоянной Холла методом Стьюдента:

где  N – число измерений.

4. ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ

1.      Назвать основные части установки и объяснить их назначение.

2.  Объяснить, с какой целью в процессе измерений изменяется направление тока, текущего через электромагнит.

3.  Пояснить, как в работе определяется величина индукции магнитного поля?

4.  Привести порядок выполнения работы.

5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ

1.      Дать определение эффекта Холла.

2.      Пояснить механизм возникновения ЭДС Холла в металлах.

3.      Вывести формулу для определения поля Холла и ЭДС Холла в металлах.

4.      Указать, от каких причин зависит постоянная Холла в металлах.

5. Объяснить, чем отличаются механизмы возникновения ЭДС Холла в металлах и полупроводниках?

6.  От каких величин зависит постоянная Холла в полупроводниках?

Рекомендуемая литература

1. Трофимова Т.И. Курс физики. - М.: Высш. шк, 2002. - 542 с.

2. Савельев И.В. Курс общей физики. Кн.5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. - М.: АСТ, 2001. - 368с.

3. Детлаф А.А., Яворский Б.М. Курс физики. - М.: Высш. шк., 2002. - 718 с.