|
Лабораторная работа № 402 ОПРЕДЕЛЕНИЕ
КОНТАКТНОЙ РАЗНОСТИ Цель работы: определить контактную разность потенциалов между полупроводником и металлом в точечном германиевом диоде. Приборы и принадлежности: термостат (колба с водой), термометр, исследуемый диод, измерительный мост, электрическая плитка. 1. ТЕОРЕТИЧЕСКОЕ
ВВЕДЕНИЕ Если два различных материала привести в соприкосновение друг с другом, то между ними возникает разность потенциалов, называемая контактной. Контактная разность потенциалов обусловлена тем, что при соприкосновении двух разных тел часть электронов из одного тела переходит в другое. В результате одно тело, из которого «ушли» электроны, заряжается положительно, а другое - отрицательно. Характеристикой
твердого тела, необходимой при описании контактной разности потенциалов,
является работа выхода. Работа выхода
-
это наименьшая энергия, которую необходимо сообщить электрону для того, чтобы
удалить его из твердого тела в вакуум. Работу выхода принято обозначать через
Рассмотрим явления в контакте металл - полупроводник. Для этого возьмем германиевый полупроводник n-типа, в котором основными носителями электрического заряда являются электроны, с работой выхода Аn и металл с работой выхода Ам.
Если Ам>Аn,,то при контакте металла с полупроводником электроны из полупроводника будут переходить в металл, так как уровень Ферми[1] в полупроводнике перед соединением с металлом лежал выше, чем в металле (Fn > FМ, см. рис.1 а, где на схеме энергетических уровней полупроводника: DW – ширина запрещенной зоны, WB – верхняя граница валентной зоны, WC – нижняя граница зоны проводимости). При этом металл заряжается отрицательно, а полупроводник - положительно, что приводит к появлению встречного потока электронов из металла в полупроводник. Направленный поток электронов из полупроводника в металл будет иметь место до тех пор, пока уровни Ферми не выровняются. После этого установится динамическое равновесие, определяемое равенством потоков электронов из полупроводника в металл и из металла в полупроводник (см. рис.1 б), и между металлом и полупроводником возникнет контактная разность потенциалов где АМ и Аn - работа выхода электрона из металла и полупроводника, соответственно. Из-за
возникновения контактной разности потенциалов jк
электрон, переходя из полупроводника в металл, должен преодолеть
потенциальный барьер, величина которого по модулю равна препятствует дальнейшему переходу электронов из полупроводника в металл. Устанавливается динамическое равновесие, при котором потоки электронов в металл и обратно сравниваются. Вследствие
малой концентрации электронов проводимости в полупроводнике (порядка При d = 10-6 м и jк » 1 В напряженность электрического поля контактного слоя Ек = jк /d » 106 В/м, т.е. приблизительно на два порядка ниже напряженности внутреннего поля кристалла, определяющего энергетический спектр полупроводника. Поэтому контактное поле не может очень сильно повлиять на структуру этого спектра (например, на ширину запрещенной зоны, на энергию активации примесей и т.д.) и его действие сводится лишь к параллельному искривлению всех энергетических уровней полупроводника в области контакта (рис.1 б). Так как в случае контакта уровни Ферми совпадают, а работы выхода - величины постоянные, то при АМ > Аn энергия электронов в контактном слое полупроводника больше, чем в остальном объеме. Поэтому в контактном слое дно зоны проводимости поднимается вверх, удаляясь от уровня Ферми. Соответственно происходит и искривление верхнего края валентной зоны. Помимо рассмотренного выше примера возможны еще следующие три случая контакта металла с примесными полупроводниками: а) АМ < Аn, полупроводник n-типа; б) АМ > Ар, полупроводник р-типа; в) АМ < Ар, полупроводник р-типа. Соответствующие зонные схемы представлены в [1]. Запирающий контактный слой обладает односторонней (вентильной) проводимостью, т.е. при приложении к контакту внешнего электрического поля он пропускает ток практически в одном направлении: либо из металла в полупроводник, либо из полупроводника в металл. Это важнейшее свойство запирающего слоя объясняется зависимостью его сопротивления от направления внешнего поля. Если к
выпрямляющему контакту (рис.2 б) электронного полупроводника с
металлом приложить внешнее напряжение U в направлении, совпадающем
с контактной разностью потенциалов (плюс источника подан на полупроводник),
то потенциальный барьер со стороны полупроводника увеличится на величину где
Если к
выпрямляющему контакту приложить внешнее напряжение U в
направлении, противоположном контактной разности потенциалов (минус источника
подан на полупроводник), то потенциальный барьер со стороны полупроводника
уменьшится на величину где Для описания процесса прохождения носителей заряда через потенциальные барьеры, возникающие на контакте металл-полупроводник, можно привлечь два механизма: квантово-механический туннельный эффект и надбарьерное прохождение носителей заряда с достаточной для этого перехода энергией. Если слой объемного заряда в полупроводнике становится чрезвычайно тонким (толщина барьера много меньше длины свободного пробега носителей заряда: d << l), то основную роль начинает играть туннельный эффект. При изучении вольтамперной характеристики выпрямляющего контакта металл-полупроводник рассмотрим надбарьерное прохождение носителей заряда через контакт, пренебрегая туннельным эффектом. Если барьер не очень велик, т.е. длина свободного пробега электронов сравнима с толщиной барьера d ~ l, то электроны проходят через барьер, испытывая лишь малое число столкновений с решеткой. При этом запирающий слой подобен вакуумному промежутку между электродами электронной лампы. В связи с этим теория, используемая в данном случае для расчета вольтамперной характеристики контакта, называется диодной. В этом случае задача о вычислении тока сводится к задаче о вычислении тока термоэлектронной эмиссии с поверхности полупроводника в металл и обратно из металла в полупроводник с учетом приложенного внешнего напряжения. Итак, величина результирующего тока I, обусловленного эмиссией электронов из полупроводника в металл I1 и обратно из металла в полупроводник I2, равна где IS - ток насыщения диода: В = 1,2×106 А/K2 - универсальная константа, Т - температура, k - постоянная Больцмана. Уравнение (5), выражающее зависимость тока от величины и знака приложенного напряжения, есть уравнение вольтамперной характеристики выпрямляющего контакта металл-полупроводник: +U соответствует прямому включению внешнего напряжения, -U - обратному. Из формулы
(5) видно, что при Т = const и прямом включении
напряжения +U
ток через контакт растет по экспоненте (рис.3). При обратном (запорном) включении напряжения -U ток сначала
возрастает и при достаточно большом U стремится к
предельному значению, численно равному току
насыщения IS. При большой величине
обратного напряжения Uпр начинают играть роль дополнительные процессы:
увеличение числа носителей тока за счет сильного поля (электростатическая и
ударная ионизация), разогревание контакта и др., которые приводят к очень
большому нарастанию обратного тока и пробою запирающего слоя. При этом ток
резко возрастает, а напряжение на контакте падает (см. рис.3). Ток через контакт в прямом направлении в несколько
десятков или сотен раз больше тока в обратном направлении при одном и том же
значении на Таким образом, если пренебречь величиной обратного тока по сравнению с величиной прямого тока (Iобр << Iпр), то можно считать, что контакт металл-полупроводник пропускает, в частности, переменный электрический ток только в одном направлении, т.е. выпрямляет его (в нашем случае, когда «-» источника подключен к полупроводнику, а «+» - к металлу, см. рис.2 в). Выпрямляющие свойства контакта используются для изготовления точечных диодов, широко применяемых в радиотехнике, вычислительной технике и интегральных схемах для получения сверхвысоких частот. 2. ОПИСАНИЕ РАБОЧЕЙ УСТАНОВКИ И МЕТОДА Для получения расчетных соотношений метода измерения контактной разности потенциалов jк между полупроводником и металлом продифференцируем выражение (5) по напряжению U и найдем дифференциальное сопротивление R0 контакта при нулевом смещении (U » 0) в зависимости от температуры: Откуда с учетом (6) где
пературы по сравнению со вторым слагаемым в уравнении (8). Измерив на опыте сопротивление R0 (например, с помощью мостиковой схемы) при разных температурах Т, а затем, построив график зависимости lnR0 от 1/T, получим прямую линию (см. рис.4). По угловому коэффициенту этой прямой, пренебрегая зависимостью lnC от температуры, в указанных координатах найдем контактную разность потенциалов:
где R01, R02 - дифференциальные сопротивления контакта при температурах Т1 и Т2, соответственно. Блок-схема установки для определения температурной зависимости сопротивления точечного диода представлена на рис.5. Исследуемый диод 1, включенный в измерительное плечо переменного тока моста 2, опускают вместе с термометром 3 в стеклянную колбу с водой 4 (как это показано на рис.5) и нагревают с помощью электроплитки 5 от комнатной температуры до 80 °С.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И 1. Включить измерительный мост в
режиме измерений на переменном токе (~) и измерить сопротивление диода при комнатной
температуре. Все измерения сопротивления проводить только
на пределе «грубо»! 2. Включить электроплитку и измерить сопротивление диода при другой температуре, меняя ее значение через каждые 5°С до 80°С. 3. Выключить цепь. Внимание! Во избежание перегрева контакта металл-полупроводник сразу после окончания измерений с помощью лапки штатива поднять из воды термометр вместе с диодом. 4. Данные занести в таблицу результатов и провести необходимые расчеты. 5. Построить график зависимости 6. По формуле (9) найти значение контактной разности потенциалов jк, определив координаты двух точек прямолинейного отрезка в начале и в конце прямой. Таблица результатов
4. ВОПРОСЫ ДЛЯ ДОПУСКА К РАБОТЕ 1. Изложить методику измерения сопротивления диода и определения контактной разности потенциалов. 2. Объяснить, как зависит сопротивление контактного слоя от температуры? От обратной температуры? 3. В каких пределах в данной работе нужно измерить температуру образца? 5. ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 1. Дайте понятие работы выхода (А), энергии Ферми (F) и контактной разности потенциалов (jк). 2. Раскройте механизм возникновения контактной разности потенциалов на границе металл-полупроводник, используя схему энергетических уровней. 3. Почему при наложении внешнего поля контакт металл-полупроводник обладает выпрямляющим свойством? 4. Выведите рабочую формулу для расчета контактной разности потенциалов. 5. Поясните вольтамперную характеристику точечного диода. Рекомендуемая
литература 1. Трофимова Т.И. Курс физики. - М.: Высш. шк, 2002. - 542 с. 2. Савельев И.В. Курс общей физики. Кн.5. Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. - М.: АСТ, 2001. - 368 с. 3. Лысов В.Ф. Практикум по физике полупроводников. - М.: Просвещение, 1976. - 207 с. 4. Шалимова К.В. Физика полупроводников. - М.: Энергия, 1971. - 312 с. 5. Лабораторный практикум по физике / Б.Ф. Алексеев, К.А. Барсуков, И.А. Войцеховская и др.; под редакцией К.А. Барсукова и Ю.И. Уханова. - М.: Высш. шк., 1988. - 351 с. |



 пряжения
(см. рис.3).
пряжения
(см. рис.3).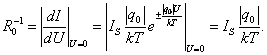

 функция, которая слабо зависит от тем-
функция, которая слабо зависит от тем-
 ,
,