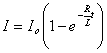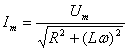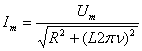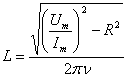Лабораторная работа № 49

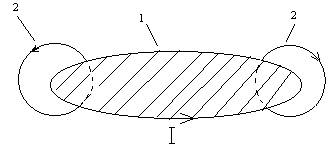
ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ СОЛЕНОИДА

Цель работы - определение индуктивности соленоида по его сопротивлению переменному току.

Приборы и принадлежности: исследуемый соленоид, звуковой генератор, электронный осциллограф, миллиамперметр переменного тока, соединительные провода.

Явление самоиндукции. Индуктивность

Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий проводящий контур. В частности, если электрический ток течет в проводящем контуре, то он создает пронизывающий этот контур магнитный поток Ф.

При изменении силы тока I в любом контуре изменяется и магнитный поток Ф, вследствие этого в контуре возникает электродвижущая сила (ЭДС) индукции, которая вызывает дополнительный ток (рис. 1, где 1 - проводящий замкнутый контур, 2 - силовые линии магнитного поля, создаваемого током контура). Это явление называется самоиндукцией, а дополнительный ток, вызываемый ЭДС самоиндукции, – экстратоком самоиндукции.

Явление самоиндукции наблюдается в любой замкнутой электрической цепи, в которой протекает элетрический ток, при замыкании или размыкании этой цепи.

Рассмотрим, от чего зависит величина ЭДС ε_s самоиндукции. Магнитный поток Ф, пронизывающий замкнутый проводящий контур, пропорционален магнитной индукции В магнитного поля, создаваемого током, протекающим в контуре, а индукция В пропорциональна силе тока.

Рис. 1

Тогда магнитный поток Ф пропорционален силе тока, т.е.

Ф = L · I,                                            (1)

где L - индуктивность контура, Гн (Генри).

Из (1) получим

L = Ф/I .                                              (2)

Индуктивностью контура L называется скалярная физическая величина, равная отношению магнитного потока Ф, пронизывающего данный контур, к величине силы тока, текущего в контуре.

Генри - это индуктивность такого контура, в котором при силе тока в 1А возникает магнитный поток 1Вб, т.е. 1 Гн = 1.

Согласно закону электромагнитной индукции

.                                                    (3)

Подставляя (1) в (3), получим ЭДС самоиндукции:

.                                                  (4)

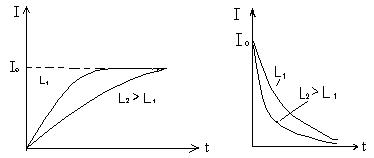
Формула (4) справедлива при L=const.

Опыт показывает, что при увеличении индуктивности L в электрической цепи сила тока в цепи увеличивается постепенно (см. рис. 2), а при уменьшении L сила тока уменьшается так же медленно (рис. 3).

Сила тока в электрической цепи при замыкании изменяется по закону , а при размыкании – по закону .

Кривые изменения силы тока показаны на рис. 2 и 3.

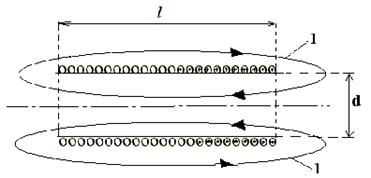
Рис. 2                                     Рис.3

Индуктивность контура зависит от формы, размеров и деформации контура, от магнитного состояния среды, в которой находится контур, а также от других факторов.

Найдем индуктивность соленоида. Соленоид - это цилиндрическая трубка, изготовленная из немагнитного непроводящего материала, на которую плотно, виток к витку,  намотана тонкая металлическая проводящая проволока. На рис. 4 показан разрез соленоида вдоль цилиндрической трубки по диаметру (1 - силовые линии магнитного поля).

Рис. 4

Длина l соленоида намного больше, чем диаметр d, т.е.
l>> d. Если l< d, то соленоид можно рассматривать как короткую катушку.

Диаметр тонкой проволоки намного меньше, чем диаметр соленоида. Для увеличения индуктивности внутрь соленоида помещают ферромагнитный сердечник с магнитной проницаемостью μ. Если l>>d, то при протекании тока внутри соленоида возбуждается однородное магнитное поле, индукция которого определяется формулой

В=μ_о μnI,                                                   (5)

где μ_о = 4π·10^-7 Гн/м – магнитная постоянная; n = N/l – число витков единицы длины соленоида; N – число витков соленоида.

Вне соленоида магнитное поле практически равно нулю. Поскольку соленоид имеет N витков, то полный магнитный поток ψ (потокосцепление), пронизывающий поперечное сечение S соленоида, равен

Ψ = NФ = NВS,                                         (6)

где Ф = BS – поток, пронизывающий один виток соленоида.

Подставляя (5) в (6) и с учётом того, что N = nl, получим

Ψ = μ_о μn² lSI .                                          (7)

С другой стороны,

Ψ = LI .                                                      (8)

Сравнивая (7) и (8), получим

L = μ_о μn² lS = μ_о μS.                                     (9)

Площадь сечения соленоида равна

.                                          (10)

С учётом (10) формула (9) запишется в виде

L = μ_о μ.                                 (11)

Определить индуктивность соленоида можно, подключив соленоид в электрическую цепь переменного тока с частотой ω. Тогда полное сопротивление (импеданс) определится формулой

,                                (12)

где R – активное сопротивление, Ом;  = х_L – индуктивное сопротивление;  = х_с – ёмкостное сопротивление конденсатора с

ёмкостью С.

Если в электрической цепи отсутствует конденсатор, т.е. электроёмкость цепи мала, то х_с<< х_L и формула (12) будет иметь вид

 .                                            (13)

Тогда закон Ома для переменного тока запишется в виде

,                                           (14)

где I_m , U_m – амплитудные значения силы тока и напряжения.

Так как ω = 2πν, где ν – частота колебаний переменного тока, то (14) примет вид

.                                       (15)

Из (15) получим рабочую формулу для определения индуктивности:

.                                          (16)

Ход работы

Для выполнения работы собрать цепь по схеме рис. 5.

1. Установить на звуковом генераторе частоту колебаний, указанную преподавателем.

2. Измерить с помощью осциллографа амплитуду напряжения U_m и частоту .

3. С помощью миллиамперметра определить действующее значение силы тока в цепи ; пользуясь соотношением  и решая его относительно I_e, определить амплитуду тока в цепи.

Рис. 5

4. Данные занести в таблицу.

Таблица

6. По формуле (16) рассчитать индуктивность соленоида.

7. По формуле (11) рассчитать проверочное значение индуктивности соленоида, исходя из его геометрии и числа витков.

Справочные данные: активное сопротивление соленоида
R = 56 Ом; длина соленоида l = 40 см; диаметр соленоида
d = 2 см; число витков соленоида N = 2000.

Рекомендуемая частота переменного тока .

Вопросы для допуска к работе

1.      Сформулируйте цель работы.

2.      Дайте определение индуктивности?

3.      Какова единица измерения индуктивности?

4.   Запишите рабочую формулу для определения индуктивности соленоида.

Вопросы для защиты работы

1. Получите формулу для определения индуктивности соленоида, исходя из его геометрических размеров и числа витков.

2. Что называется импедансом?

3. Как связаны между собой максимальное и действующее значения силы тока и напряжения в цепи переменного тока?

4. Выведите рабочую формулу индуктивности соленоида.

5. Опишите явление самоиндукции.

6. Каков физический смысл индуктивности?