Лабораторная работа № 47

ИЗУЧЕНИЕ
 ВЫНУЖДЕННЫХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ
И СНЯТИЕ СЕМЕЙСТВА РЕЗОНАНСНЫХ КРИВЫХ

Цель работы - изучение вынужденных электрических колебаний и явления резонанса в электрических цепях; снятие семейства амплитудных резонансных кривых.

Приборы и принадлежности: звуковой генератор, милливольтметр переменного тока, микроамперметр переменного тока, конденсатор, катушка индуктивности, набор резисторов или магазин сопротивлений, соединительные провода.

Вынужденные электрические колебания

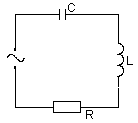
Пусть к электрической цепи, изображенной на рис. 1 и состоящей из последовательно соединенных конденсатора с электроемкостью С, катушки индуктивностью L и активного сопротивления R, подключен источник переменного тока с ЭДС, изменяющейся по закону

,                                  (1)

где - амплитуда ЭДС; - циклическая частота.

 Рис. 1

В катушке L возникает ЭДС самоиндукции, которая определяется формулой

,                                      (2)

где L - индуктивность катушки;  - скорость изменения силы тока в цепи.

В результате в такой цепи наблюдаются вынужденные электрические колебания и резонанс колебаний.

Найдем уравнения вынужденных колебаний. Цепь, состоящая из конденсатора С и катушки L, называется к о л е б а т е л ь н ы м    к о н т у р о м (см. работу № 46).

Используя второй закон Кирхгофа, получим уравнение

,

или с учетом того, что напряжение на конденсаторе , а сила тока

, получим

 .                          (3)

Поделив (3) на L и учитывая выражения (коэффициент затухания) и  (циклическая частота собственных колебаний),

формулу (3) можно записать в виде

 .                     (4)

Это дифференциальное уравнение второго порядка вынужденных колебаний.

Решение уравнения (4) следует искать в виде

,                                  (5)

где φ и ω - начальная фаза и циклическая частота вынужденных колебаний; q_о - амплитуда заряда на обкладке конденсатора,

,

 .                          (6)

Сила тока равна , и с учетом

 выражений  (сдвиг фазы между током и ЭДС источника тока)

и  получим

,                                 (7)

где                  ;                (8)

.                                      (9)

Если в (8) и (9) подставим ; , то получим

;                    (8^/)

.                                   (9^/)

Напряжения в цепи изменяются по закону:

- на активном сопротивлении R

;                  (10)

- на конденсаторе с учетом , ,  и (4)

.                     (11)

- ЭДС самоиндукции, или напряжение в катушке,

.                   (12)

В формуле (8^/) выражение

                         (13)

называется импедансом, т.е. полным сопротивлением электрической цепи, а

                                            (14)

и                                                                                  (15)

называются и н д у к т и в н ы м   и   е м к о с т н ы м сопротивлениями (реактивными сопротивлениями). Тогда с учетом (13) формулу (8^/) можно записать

.                                           (16)

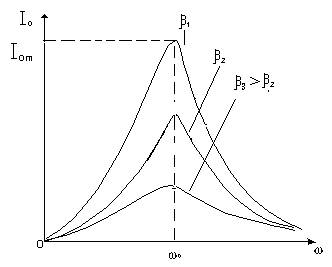
Формула (8^/), или (16), соответствует закону Ома для амплитудных значений переменного тока. Амплитудное значение силы тока I_o зависит от ω, L, C и R.

Исследуем зависимость I_o от ω.

При ω→0 I_o→0, при ω→∞ I_o также стремится к нулю, т.е. I_o→0.

Приравнивая  нулю, найдем резонансную частоту, которая не

зависит от R и равна

.                              (17)

При этой частоте из (8) следует, что максимальное значение амплитуды силы тока равно

.                                         (18)

С ростом R, а следовательно, коэффициента затухания , I_om уменьшается.

Зависимость резонансных кривых I_o от ω показана на рис. 2.

Рис. 2

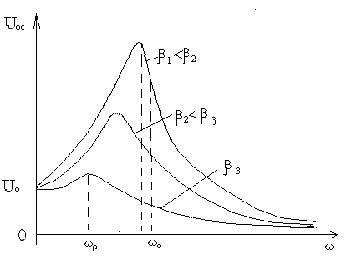
Резонансные кривые амплитудных значений напряжения отличаются от резонансных кривых силы тока.

На рис. 3 приведена зависимость изменения резонансных кривых между обкладками конденсатора от частоты ω и коэффициента затухания β.

Рис. 3

Из рис. 3 видно, что при ω→0 амплитудное значение напряжения U_oc стремится к U_o=ε_o. Резонанс колебаний напряжения U_oc наступает при частоте

.                 (19)

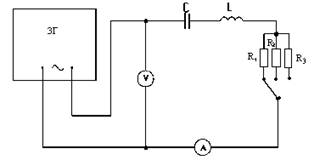
Изучить резонанс колебаний силы тока можно, собрав электрическую цепь по схеме, представленной на рис. 4.

Рис. 4

Ход работы

1. Установить на звуковом генераторе начальное значение частоты

2. С помощью регулятора напряжения установить на выходе звукового генератора напряжение, равное 30 мВ.

3. Включить в цепь последовательно с катушкой L и конденсатором C сопротивления (сначала R₁, затем R_2, R₃ ).

4. Измерить значения силы тока I₁, I₂, I₃, изменяя значения частоты в интервале от 200 до 2000 Гц через каждые 200 Гц, поддерживая напряжение в цепи неизменным с помощью регулятора напряжения. Результаты измерений занести в таблицу.

Таблица

4. По результатам измерений на миллиметровой бумаге построить семейство амплитудных резонансных кривых.

5. По полученному графику зависимости I_o от () и по максимальному значению силы тока I_om определить резонансную частоту .

6. По формуле

                               (20)

рассчитать значение резонансной частоты , подставляя параметры L и C электрической цепи.

7. Сравнить экспериментальное значение  и рассчитанное по формуле (20) значение .

Вопросы для допуска к работе

1.      Сформулируйте цель работы.

2.      Какие колебания называются свободными?

3.      Какие колебания называются вынужденными?

4.      Запишите дифференциальное уравнение вынужденных колебаний.

5.      Что называется резонансом колебаний?

Вопросы для защиты работы

1.      Что называется колебательным контуром? Объясните возникновение вынужденных электрических колебаний в цепи переменного тока.

2.      Выведите закон Ома для электрической цепи переменного тока, содержащей омическое сопротивление, емкость и индуктивность.

3.      Получите дифференциальное уравнение вынужденных электрических колебаний.

4.      Выведите формулу для резонансных частот колебаний силы тока и напряжения.

5.      Изобразите и поясните ход резонансных кривых (амплитудных и фазовых).

6.      Что такое полное сопротивление (импеданс) переменной электрической цепи?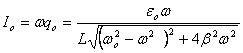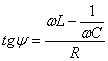