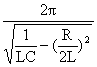Лабораторная работа № 46

Затухающие электрические колебания

Цель работы - наблюдение и изучение затухающих электрических колебаний с помощью осциллографа: определение периода колебаний, влияние параметров колеба­тельного контура L, C, R на характер затухающих колебаний.

Приборы и принадлежности: осциллограф, набор колебательных контуров с изменяемыми параметрами L, C, R; генератор прямоугольных импульсов.

Затухающие электрические колебания

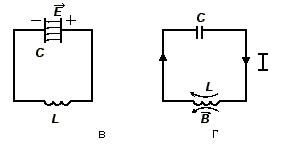
Замкнутая цепь, состоящая из катушки индуктивностью L и конденсатора емко­стью C, представляет собой колебательный контур (рис. 1).

Предложим, что мы, разомкнув контур, зарядили конденсатор. Между пластинами конденсатора появится электрическое поле, которое будет обладать энергией  (рис. 1, а). Замкнем теперь кон-

денсатор на катушку  с индуктивностью. Конденсатор начнет раз­ряжаться, и его электрическое поле будет уменьшаться. При этом в контуре возникнет электрический ток разряда конденсатора, а  в цепи потечет ток, отчего в катушке  появится маг­нитное поле.  Но за счет явления самоиндукции, наблюдаемой в катушке  L, ток в цепи нарастает медленно. Через время, равное четверти периода колебаний, конденсатор разрядится полностью и электрическое поле исчезнет, в этот момент времени ток в цепи будет максимальный.  Но магнитное поле в катушке при этом достигнет максимума, а следовательно, энергия электрического поля переходит  в энергию магнитного поля, определяемую формулой  (рис.1 б).

Рис. 1

В дальнейшие моменты времени магнитное поле будет исчезать, т.к. ток в цепи уменьшится до нуля. Это исчезающее поле вызовет экстраток самоиндукции, который в соответствии с законом Ленца будет стремиться поддерживать ток разряда. Поэтому конденсатор по отношению к первичному направлению тока будет перезаряжаться и между его пласти­нами появится электрическое поле противоположного направления. Через время, равное половине периода колебаний, магнитное поле исчезнет, ток в цепи равен нулю  электрическое поле достигнет максимума, а энергия магнитного поля вновь превратится в энергию электрического поля (рис.  1в). В дальнейшем конденсатор будет снова разряжаться, и в контуре возникнет ток, направ­ленный противоположно току в предыдущей стадии процесса. Через время 3/4 Т конден­сатор вновь окажется разряженным, а энергия электрического поля превратится в энергию магнитного поля (рис. 1, г) и  ток в цепи  станет максимальным. Через промежутки времени, равные полному периоду колебаний Т, электрическое состояние контура будет таким же, как и в начале колебаний (рис. 1, а).

Если сопротивление контура равно нулю, то указанный процесс периодического превращения энергии электрического поля в энергию магнитного поля и обратно будет продолжаться неограниченно долго, и мы получим собственные незатухающие электриче­ские колебания.

Всякий реальный контур обладает активным сопротивлением, вследствие этого энергия, первоначально запасенная в конденсаторе, непрерывно расходуется на выделение джоулева тепла, так что амплитуда колебаний постепенно уменьшается и в конце концов колебания в контуре прекращаются. В этом случае в контуре наблюдаются свободные затухающие электрические колебания. Найдем закон изменения силы тока и напряжения.

Запишем для контура (рис. 2) второй закон Кирхгофа:

U_R + U_C = ε,                                            (1)

где U_R = IR – падение потенциала на сопротивлении R;  – падение потенциала на обкладках конденсатора; C – емкость конденсатора;  – ЭДС самоиндукции, возникающая в катушке;

L – индуктивность катушки.

Подставляя выражения  U_R, U_C и ε в (1), получим

,

так как , а , , то получим

.                               (2)

Рис. 2

Уравнение (2) – дифференциальное уравнение затухающих колебаний.

Обозначив

;               ,                                 (2а)

где – коэффициент затухания;  – частота собственных коле

баний контура.  Уравнение (2) с учетом (2а) можно записать в виде

= 0.                               (3)

Найдем решение уравнения (3):

,   (4)

где  – частота затухающих колебаний; U₀,

₀ – амплитуда и начальная фаза затухающих колебаний.

Величина U₀ выражает амплитуду затухающих колебаний.

Затухание колебаний происходит тем быстрее, чем больше омическое сопротивление контура R и чем меньше индуктивность.

Период затухающих колебаний T определяется формулой

T=.

Подставляя сюда вместо w₀ и  (2а), получим

T₁=.                                  (5)

В случае свободных незатухающих колебаний активное сопротивление контура равно нулю. Отсюда получим известную формулу Томсона

T₂ = 2.                                           (6)

Амплитуда затухающих колебаний падения потенциала на конденсаторе

U_с=,                                         (7)

которая меняется во времени по экспоненциальному закону (рис. 3), где U_o – значение амплитуды напряжения в момент времени t=0.

Рис. 3

Отношение соседних амплитуд, отстоящих друг от друга на время, равное одному периоду, называется декрементом затухания :

,

а логарифм этого отношения – логарифмическим декрементом затухания :

.                        (8)

Из формулы (8) получим

T₂=.                              (9)

При медленных затухающих колебаниях R мало по сравнению с L, и для периода колебаний справедлива формула (6). В этом случае формулу (8) с учетом (6) можно записать в виде

.                                 (10)

Ход работы

Осциллограммы затухающих колебаний можно получить с помощью установок, схемы которых приведены на рис. 4 и 5.
Рис. 4 – схема установки с генератором прямоугольных импульсов. Рис. 5 – схема установки с осциллографом, имеющим генератор прямоугольных импульсов (рис. 5).

Рис. 4

Рис. 5

1. Включить установку, собранную по одной из схем, приведенных на рис. 4 и 5.

1.      Выбрать в соответствии с таблицей (или по указанию преподавателя) фиксированные параметры L, R и, меняя параметр C колебательного контура, изучить зависимость периода колебаний T от величины емкости колебательного контура.

3. В графу «Т» занести значение периода колебаний, измеренное с помощью электронного осциллографа. В графу «Т₁» - значение периода затухающих колебаний, рассчитанное по формуле (5), а в графу «Т₂» - значение периода колебаний, рассчитанное по формуле (6).

4. Точно так же выбрать фиксированные значения C и R,  меняя параметр L колебательного контура изучить зависимость периода колебаний от величины индуктивности контура.

5. Выбрав фиксированные значения C и L,  меняя значение R изучить зависимость периода колебаний от сопротивления контура.

6. Зарисовать на кальку осциллограммы затухающих колебаний для тех же значений параметров L,C,R колебательного контура, затем перенести их на миллиметровую бумагу.

7. Измерить в миллиметрах величины соседних амплитуд , отстоящих друг от друга на время равное одному периоду колебаний.

8. По формуле

                                               (11)

рассчитать измеренное значение логарифмического декремента затухания.

9. По формуле (8) рассчитать значение логарифмического декремента затухания, исходя из параметров колебательного контура,  и сравнить со значением (11).

Таблица

10. На основании полученных данных сделать вывод о том, как влияют изменения параметров L, C, R колебательного контура на процесс затухания колебаний.

Вопросы для допуска к работе

1. Какова цель работы?

2. Что представляет собой колебательный контур?

3. Что называется декрементом затухания, логарифмическим декрементом затухания?

4. Опишите предложенные методы измерения периода затухающих колебаний.

Вопросы для защиты работы

1. Опишите электрические колебания, возникающие в колебательном контуре.

2. Запишите уравнения и начертите графики:

а) собственных незатухающих электрических колебаний в контуре;

б) затухающих электрических колебаний в контуре.

3. Выведите формулу периода затухающих колебаний.

4. Как связан логарифмический декремент затухания с периодом колебания?

5. Выведите формулу периода незатухающих колебаний.

6. Как влияют величины сопротивления, емкости и индуктивности на частоту (период) собственных колебаний в контуре?

7. Как влияет на быстроту затухания колебаний величина сопротивления, емкости, индуктивности контура?