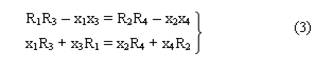Лабораторная работа № 33

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА
С ПОМОЩЬЮ С-МОСТА УИТСТОНА

Цель работы - изучение работы С-моста Уитстона и определение емкости конденсаторов; определение емкости конденсаторов при их последовательном и параллельном соединениях.

Приборы и принадлежности: набор конденсаторов неизвестной емкости, магазин емкости, реостат, источник питания, осциллограф или нуль-индикатор.

Теория электрического моста

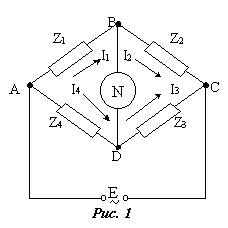
Предварительно необходимо изучить теоретическую часть лабораторной работы № 31.

Принципиальная схема четырехплечевого (одинарного) моста приведена на рис. 1. Плечи моста АВ, ВС, СD, DА содержат в общем случае комплексные сопротивления, т.е. включают в себя как активные сопротивления, так и емкостные  и индуктивные. Питание моста осуществляется от источника переменного тока Е, подключенного к диагонали АС; в диагональ ВD включен индикатор  N  : либо гальванометр, либо осциллограф.

Мост называется сбалансированным, или уравновешенным, если ток в измерительной диагонали ВD равен нулю, то есть, когда потенциалы точек В и D равны друг другу, совпадают как по фазе, так и по амплитуде. Это  имеет место при равенстве разностей потенциалов  U₁ = U₄ на сопротивлениях Z₁ и Z₄.

Определим разности потенциалов  в случае сбалансированного моста.

Так как ток в диагонали индикатора равен нулю, то из первого закона Кирхгофа следует, что комплексные силы тока равны соответственно: İ₁=İ₂, İ₃=İ₄.

Далее из закона Ома определим силы тока:

İ₁ = İ₂ = ;                    İ₃ = İ₄ = ,

где Z_i – комплексное сопротивление; Е – электродвижущая сила.

Отсюда легко найти U₁ и U₄:

U₁ = İ₁Ζ₁ = ;                       U₄ = İ₄Z₄ = .

Так как U₁ = U₄, получим

 Z₁Z₃ = Z₂Z₄.                                (1)

Из (1) следует, что в случае уравновешенного моста между комплексными сопротивлениями имеет место вполне определенное соотношение, а именно: в сбалансированном мосте произведения полных сопротивлений противолежащих плеч равны. Это позволяет вычислить измеряемое сопротивление, если известны сопротивления трех других плечей. Комплексные сопротивления можно представить в виде

Z₁= R₁ + ix₁;       Z₂ = R₂ + ix₂;

Z₃ = R₃+ ix₃;        Z₄ = R₄ + ix₄,                            (2)

где R_1, R₂, R_3, R₄ – активные сопротивления; x_1, x_2, x_3, x₄ – реактивные (емкостное или индуктивное сопротивления);  i – мнимая единица
(i = ).

Подставив выражения  Z₁, Z₂, Z₃ и Z₄ в (1), получим:

 R₁R₃ + i (R₁x₃ + R₃x₁) – x₁x₃ = R ₂R₄ + i (R₄x₂ + R₂x₄) – x₂x₄.

При выполнении условия

обеспечивается равенство потенциалов в точках B и D по амплитуде и по фазе.

В данной работе рассматривается  С-мост Уитстона,  позволяющий  проводить измерения величин емкости конденсаторов. Схема С-моста Уитстона, где в качестве индикатора применен осциллограф, приведена на рис. 2.

Рис. 2

Сравнивая данную схему с рис. 1, заметим, что точки А, В, С, D на рис. 2 соответствуют аналогичным точкам на рис. 1. Следовательно, выражения (2) можно записать в виде

Z₁ = R₁+ ix₁ = r₁,

где R₁ = r₁, x₁ = 0, r₁ – сопротивление левого плеча реостата
(по схеме рис. 2), реактивное сопротивление х₁ равно нулю;

Z₂ = R₂ + ix₂ = ix₂,

где R₂ = 0; x₂ = – величина реактивного сопротивления

неизвестной емкости переменному току частотой  (в нашем случае  – частота тока в промышленной сети, равная 50 Гц);

Z₃ = R₃ + ix₃= ix₃,

где R₃ = 0, х₃ =; С₀ – известная емкость конденсатора,

определяемая магазином емкости;

Z₄ = R₄ + ix₄ = r₂,

где R₄ = r₂, х₄ = 0, r₂ – сопротивление правого (по схеме) плеча реостата.

Подставляя полученные величины R_i и x_i в систему (3), получаем

– = – .                               (4)

Из уравнения (4) легко можно найти С_x:

С_х = С₀ּ.                                  (5)

Поскольку сопротивление любого металлического неферромагнитного и изотропного проводника определяется формулой
r =, то

r₁=;               r₂=.                      (6)

Подставляя (6) в (5), получим

 С_х = С₀ּ,                                 (7)

где l, s – длина и сечение проводника;  – удельное сопротивление.

Формула (7) и есть основная расчетная формула для определения величины неизвестной емкости.

Электроемкостью конденсатора называется  отношение заряда , сосредоточенного на обкладках конденсатора и разности потенциалов (U) между обкладками: .

 В данной работе l₁ и l₂ являются длинами плеч реостата.

Осциллограф в качестве нуль-индикатора используют следующим образом. У осциллографа выключают горизонтальную развертку, вследствие чего луч на экране может отклоняться только по вертикали. Это, в свою очередь, означает, что если на вход осциллографа (вход Y) подано напряжение, т.е. мост разбалансирован и разность потенциалов между точками В и D (рис. 2 или рис. 1) не равна нулю, то на экране мы видим вертикальную линию. Если же мост уравновешен, то разность потенциалов между точками В и D, а следовательно, и напряжение на входе осциллографа равны нулю и вертикальная линия на экране обращается в точку.

Ход работы

1. Собрать схему, показанную на рис. 2. В зависимости от предложенных приборов к клеммам В и D моста подключить входные клеммы либо осциллографа, либо лампового нуль-индикатора.

2. В качестве С_х подключить конденсатор неизвестной емкости С_х1.

3. Измерить величину неизвестной емкости. Для этого движок потенциометра установить вблизи середины шкалы
(с тем чтобы относительная погрешность была минимальной – см. лабораторную работу № 31) и подбором величины емкости магазина и корректировкой положения движка потенциометра уравновесить мост, т.е. добиться на экране осциллографа обращения вертикальной линии в точку.

ВНИМАНИЕ! Категорически запрещается работать с большой яркостью луча, т.к. сведение вертикальной линии в точку вызовет немедленное прогорание люминофора экрана.

Сместив движок реостата на небольшое расстояние (~1-2 см) от середины шкалы потенциометра, то в одну,  то в другую сторону, произвести еще два измерения.

Величину неизвестной емкости рассчитать по формуле (7).

4. Вместо С_х1 подключить С_х2 и измерить его величину согласно пункту 3.

5. В качестве С_х подключить поочередно соединенные последовательно и параллельно С_х1 и С_х2 и провести измерения по пункту 3.

6. По формулам

С_пар.= С_х1 + С_х2 ,              С_посл. =         (8)

проверить правильность значений емкостей, полученных при выполнении пункта 5.

Результат измерений занести в таблицу.

Таблица

Примечание. Измерение каждого значения емкости проводить не менее трех раз.

Вопросы для допуска к работе

1.   Какова цель работы?

2.      Объясните принцип действия измерительной мостовой цепи.

3.      Почему в данной работе схема питается переменным током?

4.      Оцените погрешность измерения электроемкостей.

Вопросы для защиты работы

1. Что называется электроемкостью конденсатора?

2. Выведите условие равновесия С-моста Уитстона.

3. Выведите формулы электроемкостей плоского, сферического и цилиндрического конденсаторов.

4. Нарисуйте электрическую цепь последовательного и параллельного соединения конденсаторов и получите формулы электроемкостей этих соединений.

5. Каковы Ваши критические замечания по данной работе?