ЛАБОРАТОРНАЯ РАБОТА №107

Проверка основного уравнения динамики

вращательного движения

Цель работы: Экспериментальная проверка основного закона динамики вращательного движения с помощью маятника Обербека.

Приборы и принадлежности: маятник Обербека с миллисекундомером FРМ – 15, штангенциркуль.

Теоретическое введение

При рассмотрении вращения твердого тела с динамической точки зрения наряду с понятием о силах вводится понятие о моментах сил и наряду с понятием о массе – понятие о моменте инерции.

Пусть материальная точка массой т под действием внешней силы движется криволинейно относительно неподвижной точки О. На материальную точку действует момент силы и точка обладает моментом импульса. Положение движущейся материальной точки определяется радиус-вектором , проведенным к ней из точки О (рис.1). Моментом силы  относительно неподвижной точки О называется векторная величина , равная векторному произведению радиус-вектора  вектор силы

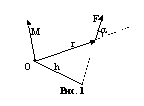Вектор  направлен перпендикулярно плоскости векторов  и  и его направление соответствует правилу правого винта. Модуль момента сил равен

где a - угол между векторами  и , h=rsina - плечо силы, равное кратчайшему расстоянию от точки О до линии действия (вдоль которой действует сила) силы .

Моментом импульса  относительно точки О называется векторная величина, равная векторному произведению радиуса вектора  на вектор импульса , то есть

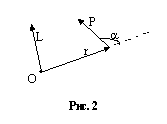
Вектор  направлен перпендикулярно плоскости векторов  и  (рис.2). Модуль момента импульса равен

где b - угол между направлением векторов  и .

Основной закон динамики вращательного движения

Пусть механическая система, состоящая из N материальных точек под действием внешних сил, результирующая которых , совершает криволинейное движение относительно неподвижной точки О, то есть

где  - радиус-вектор, проведенный от точки О до i-ой материальной точки,  - вектор силы, действующей на i-ую материальную точку.

Также можно найти момент импульса системы

где  - момент импульса i-ой материальной точки.

Момент импульса  зависит от времени t, так как скорость является функцией от времени. Взяв производную от момента импульса системы по времени t, получим

Формула (7) является математическим выражением основного закона динамики вращательного движения системы, согласно которому скорость изменения момента импульса системы по времени равна результирующему моменту внешних сил, действующих на систему.

Закон (7) справедлив и для твердого тела, т.к. твердое тело можно рассматривать как совокупность материальных точек.

 Пусть в частном случае твердое тело вращается относительно неподвижной оси, проходящей через центр масс, под действием внешней силы . Твердое тело разбиваем на материальные точки. Для материальной точки массой m_i уравнение движения запишется

Момент импульса  для i – ой материальной точки равен

Поскольку при вращательном движении b = 90⁰, то и линейная скорость  связана с угловой скоростью формулой  Тогда (9) можно записать в виде

Величина  представляет собой момент инерции материальной точки относительно оси Z. Тогда (10) примет вид

С учетом (11) основной закон динамики вращательного движения твердого тела относительно неподвижной оси запишется

где - момент инерции твердого тела относительно оси Z.

При

где  - угловое ускорение. Согласно основному уравнению динамики вращательного движения (12) результирующий момент внешней силы, действующей на тело, равен произведению момента инерции  J тела на его угловое ускорение.

Из уравнения (12) следует, что при J = const угловое ускорение тела

прямо пропорционально моменту внешних сил относительно оси вращения, т.е.

При M = const угловое ускорение обратно пропорционально моменту инерции тела, т.е.

Целью настоящей работы является проверка соотношений (13) и (14), а, следовательно, и основного уравнения динамики вращательного движения (12), следствиями которого они являются.

Описание рабочей установки и метода измерений

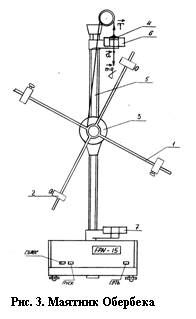
Для проверки соотношений (13) и (14) используется маятник Обербека, представляющий собой инерционное колесо в виде крестовины. На четырех взаимно перпендикулярных стержнях 1 расположены четыре одинаковых цилиндрических груза 2, которые можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси. Грузы закрепляются симметрично, т.е. так, чтобы их центр масс совпадал с осью вращения. На горизонтальной оси крестовины имеется двухступенчатый диск 3, на который наматывается нить. Один конец нити прикреплен к диску, а ко второму концу нити подвешен груз 4, под действием которого прибор приводится во вращение. Общий вид маятника Обербека FРМ-06 изображен на рис.3. Для удержания системы крестовины вместе с грузами в состоянии покоя используется тормозной электромагнит. С целью отсчета высоты падения грузов на колонне нанесена миллиметровая шкала 5. Время падения груза 4 измеряется миллисекундомером FРМ-15, к которому подключены фотоэлектрические датчики №1(6) и №2(7). Фотоэлектрический датчик №2(7) вырабатывает электроимпульс конца измерений времени и включает тормозной электромагнит.

Если предоставить возможность грузу 4 двигаться, то это движение будет происходить с ускорением a.

где t- время движения груза с высоты h. При этом шкив со стержнями и находящимися на них грузами будет вращаться с угловым ускорением e.

где r- радиус шкива.

Вращающий момент силы, приложенной к крестовине и сообщающий угловое ускорение вращающейся части прибора, находим по формуле

где Т- сила натяжения шнура. По второму закону Ньютона для груза 4 имеем

откуда

где g- ускорение свободного падения.

Из формул (12), (15), (16), (17) и (19) имеем

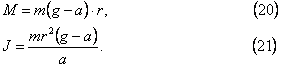
Порядок выполнения работы и обработка результатов измерений

1.      Измерить штангенциркулем радиус большого и малого шкивов r₁ и r₂.

2.      Определить массу груза 4 взвешиванием на технических весах с точностью ±0,1 г.

3.      Проверить соотношение (13). Для этого:

-          закрепить цилиндрические подвижные грузы на стержнях на ближайшем расстоянии от оси вращения так, чтобы крестовина была в положении безразличного равновесия;

-          намотать нить на большой шкив радиуса r₁ и измерить время движения груза t с высоты h миллисекундомером, для чего

-          включить сетевой шнур измерителя в сеть питания;

-          нажать клавишу «СЕТЬ» и проверить, показывают ли все индикаторы измерителя нуль и горят ли все индикаторы обоих фотоэлектрических датчиков;

-          переместить груз в верхнее положение и проверить, находится ли схема в состоянии покоя;

-          нажать клавишу «ПУСК» и миллисекундомером измерить время движения груза;

-          нажать клавишу «СБРОС» и проверить, произошло ли обнуление показаний измерителя и освобождение блокировки электромагнитом;

-          переместить груз в верхнее положение, отжать клавишу «ПУСК» и проверить, произошла ли повторная блокировка схемы;

-          опыт повторить 5 раз. Высоту h не рекомендуется менять в течение всей работы;

-          по формулам (15), (16), (20) вычислить значения a₁,e₁, М₁;

-          не меняя расположения подвижных грузов и оставляя тем самым неизменным момент инерции системы, опыт повторить, наматывая нить с грузом на малый шкив радиусом r₂;

-          по формулам (15), (16), (20) вычислить значения a₂, e₂, М₂;

-          проверить справедливость следствия основного закона динамики вращательного движения:

, при  

-          данные результатов измерений и вычислений занести в таблицы 1 и 2.

4.      Проверить соотношение (14). Для этого:

-          раздвинуть подвижные грузы до упоров на концах стержней, но так, чтобы крестовина снова была в положении безразличного равновесия;

-          для малого шкива r₂ определить время движения груза t^/ по данным 5 опытов;

-          по формулам (15), (20), (21) определить значения a^/, e^/, J₁;

-          при проверке соотношения  при  можно пользоваться значениями предыдущего опыта, положив  и ;

-          по формуле (21) определить значение J₂;

-          вычислить значения  и .

-          Результаты измерений и вычислений занести в таблицу 3.

Таблица 1

Таблица 2

Таблица 3

Вопросы для допуска к работе

1.      Какова цель работы?

2.      Сформулируйте основной закон динамики вращательного движения. Поясните физический смысл величин, входящих в данный закон, укажите единицы их измерения в «СИ».

3.      Опишите устройство рабочей установки.

4.      Оцените погрешность метода измерений величины углового ускорения.

Вопросы для защиты работы

1.      Дайте определения момента сил, момента импульса материальной точки относительно неподвижной точки О.

2.      Сформулируйте основной закон динамики вращательного движения твердого тела относительно неподвижной точки О и неподвижной оси Z.

3.      Дайте определение момента инерции материальной точки и твердого тела.

4.      Выведите рабочие формулы.

5.      Выведите соотношение  при  и  при

6.      Есть ли критические замечания к данной работе?