|
Целью лабораторного практикума «Электричество и электромагнетизм»
является изучение электромагнитных явлений, проверка на опыте их основных
закономерностей. При этом студенты сталкиваются с необходимостью практически
ознакомиться с наиболее важными приборами, овладеть основными методами электрических
измерений и научиться обрабатывать результаты, полученные при измерениях.
Данные методические указания содержат сведения и рекомендации,
позволяющие облегчить приобретение студентами этих навыков.
Классификация электроизмерительных приборов
Основные электрические приборы классифицируются по двум
признакам: по принципу действия и по роду измеряемой величины.
По принципу действия, т.е. в зависимости от природы явлений,
на которых основана работа электроизмерительных приборов, их можно разделить на следующие системы:
магнитоэлектрические приборы, электромагнитные, электродинамические,
тепловые, электростатические и другие. По роду измеряемой величины они
делятся на амперметры (для измерения тока), ваттметры (для измерения
мощности) и т.п. Рассмотрим системы приборов, используемых при выполнении
лабораторных работ.
Принцип действия приборов магнитоэлектрической системы
основан на взаимодействии магнитного поля постоянного магнита с током,
протекающим по обмотке легкой подвижной катушки. Данные приборы применяются в
качестве амперметров и вольтметров постоянного тока, а в сочетании с
выпрямительными устройствами – переменного тока. Приборы обладают высокой
точностью и имеют равномерную шкалу, т.к. отклонение стрелки прибора линейно
зависит от силы тока в катушке.
В основе принципа действия приборов электромагнитной системы
лежит взаимодействие магнитного поля тока, протекающего по обмотке
неподвижной катушки, с подвижным железным сердечником. Отклонение стрелки
прибора пропорционально квадрату величины протекающего по катушке тока. Поэтому
шкала таких приборов неравномерна. Электромагнитные вольтметры и амперметры
применяются в качестве щитовых приборов переменного и постоянного токов.
Точность этих приборов сравнительно невысока.
Принцип действия приборов электродинамической системы
основан на взаимодействии магнитных полей токов, протекающих по двум
катушкам, из которых одна подвижна, а другая неподвижна. Сила этого
взаимодействия (как и в предыдущем случае) пропорциональна квадрату силы
тока, поэтому шкала приборов этой системы тоже неравномерна. Приборы
применяются в качестве амперметров и вольтметров постоянных и переменных
токов. Точность этих приборов очень высокая.
Работа приборов электростатической системы основана на
взаимодействии электрически заряженных проводников. Под действием сил
электрического поля подвижный проводник перемещается относительно неподвижного.
Величина этого перемещения пропорциональна измеряемому напряжению. Приборы
служат преимущественно вольтметрами для измерения высоких постоянных
напряжений.
Многопредельные измерительные приборы.
Снятие показаний с прибора. Цифровые приборы
Существуют измерительные приборы, электрическую схему
которых можно переключать для изменения диапазонов (пределов) измерения.
Наличие таких многопредельных приборов обусловлено тем, что часто возникает
необходимость измерять электрические величины, изменяющиеся в очень широких
пределах, причем с достаточной степенью точности. Ниже будет показано, что
нужно стремиться к тому, чтобы указательная стрелка прибора при измерении
отклонялась от начального положения более чем на 2/3 шкалы. При этом говорят,
что стрелка находится в «зоне измерения». Исходя из этого правила, следует
каждый раз выбирать тот или иной предел измерения, переключая указатель
пределов в соответствующее положение.
Многопредельные приборы могут быть одновременно мультиметрами
(многоцелевыми или универсальными), позволяющими измерять ток и напряжение
(ампервольтметры); ток, напряжение и сопротивление (авометры) и т.д. В этом
случае приборы, наряду с переключателем пределов измерения, снабжены переключателем
рода работы.
Перед подключением прибора к электрической цепи необходимо:
1) поставить переключатель рода работы в нужное положение (измерение тока или
измерение напряжения); 2) переключатель пределов измерения поставить на
максимальное значение измеряемой величины. После включения источника электрической
энергии последовательным переключением пределов измерения от большего к меньшему нужно добиться отклонения стрелки в зону измерения.
Снятие показаний с прибора (нахождение численного значения
измеряемой величины) осуществляют (как правило) тогда, когда стрелка
находится в зоне измерения. Вначале вычисляют цену деления шкалы ω, которая для
приборов с равномерной шкалой определяется следующим образом:
ω = Хо/N, (1)
где Xо
– конечное значение предела измерения; N – полное число делений на шкале
прибора. Вычисления производят в системе СИ, т. е. значение Xо берут в амперах либо в вольтах. Затем
вычисляют значение измеряемой величины X:
Х = ω×n, (2)
где ω – цена деления; n – порядковый номер
деления, на которое указывает стрелка прибора при измерении.
В настоящее время в лабораторной практике все чаще используются
цифровые многопредельные универсальные измерительные приборы, имеющие ряд
достоинств по сравнению со стрелочными приборами: быстродействие, высокая
точность, непосредственный вывод на табло численного значения измеряемой
величины, что освобождает от необходимости проведения вычислений по формулам
(1) и (2). В современных цифровых приборах выбор предела измерения
осуществляется автоматически, экспериментатор устанавливает лишь переключатель
рода работы прибора. Все это значительно упрощает процесс измерения. Главным
достоинством цифровых приборов является возможность их сочетания с вычислительными
машинами, т.е. с системами автоматического управления.
Обозначение по шкале прибора
Все характеристики и данные, необходимые для эксплуатации
прибора, обозначены на его корпусе (шкале) условными знаками. Ниже
рассмотрены некоторые из них.
1. Род измеряемой величины: амперметр (А), миллиамперметр
(mА,
мА), микроамперметр (μА, мкА), вольтметр (В, V), милливольтметр (mV,мВ), киловольтметр (kV),
ампервольтметр (А, В) и другие.
2. Род тока I для постоянного тока (–), для переменного тока (~), для
постоянного и переменного токов ( ~ ).
 3.
Рабочее положение шкалы прибора: горизонтальное 3.
Рабочее положение шкалы прибора: горизонтальное
(⌐¬, ®)
вертикальное (^, ), наклонное (ä,
30).
   4. Напряжение, которое выдерживает
изоляция корпуса прибора (~2 kV либо 2 ), в киловольтах. 4. Напряжение, которое выдерживает
изоляция корпуса прибора (~2 kV либо 2 ), в киловольтах.
 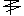 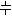 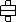 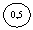       5.
Система прибора: магнитоэлектрическая ( ), электромагнитная ( ), электродинамическая ( ), электростатическая ( ) 5.
Система прибора: магнитоэлектрическая ( ), электромагнитная ( ), электродинамическая ( ), электростатическая ( )
и др.
6. Класс точности прибора: . Эта
характеристика подробнее рассматривается в следующем разделе.
Наиболее важные характеристики используемых приборов необходимо
привести в отчете о проделанной лабораторной работе. В первую очередь это
касается данных, перечисленных выше.
Погрешности электроизмерительных приборов
Для характеристики точности измерительных приборов используют
относительную погрешность измерения Е, которая в простейшем
случае определяется по формуле
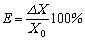 , (3) , (3)
где ΔX – абсолютная
погрешность прибора; Xо – конечное значение
данного предела измерения.
Величина относительной погрешности, выраженная в процентах,
численно равна классу точности прибора k:
Ео = k. (4)
Существуют приборы восьми классов точности в соответствии
с величиной погрешности (за счет градуировки, влияния внешних полей и других
причин), допускаемой при их использовании: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5;
2,5; 4,0. Класс точности приводится на шкале прибора.
Зная класс точности, по формулам (3) и (4) можно определить
абсолютную погрешность ∆Х для данного предела измерений:
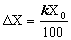 , (5) , (5)
а затем и относительную
погрешность измерения Е по формуле
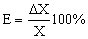 , (6) , (6)
где Х – показание прибора (значение
измеряемой величины).
Из анализа приведенных формул следует,
что класс точности показывает величину наименьшей относительной погрешности
(в процентах), которая может иметь место при измерениях посредством данного
прибора. Или еще говорят, что класс точности представляет собой
относительную погрешность измерения предельного значения, выраженную в
процентах.
Для приборов с
равномерной шкалой абсолютная погрешность при любом отклонении стрелки
одинакова. Поэтому из (6) следует, что при меньших отклонениях стрелки
относительная погрешность больше. Например, пусть у вольтметра класса точности
k=0,5 шкала содержит N=150
делений, используется предел измерения Х0=7,5
вольт, а стрелка отклонилась на n1=30 делений. Тогда по формуле (1) цена деления
ω1=0,05 В/дел., по (2) показание прибора Х1=1,5 В, по (5) абсолютная погрешность ∆Х1=0,0375
В, по формуле (6) относительная погрешность Е1= 2,5%.
Пусть теперь стрелка этого же прибора отклонилась на
n2 = 100 делений, а остальные параметры остались без изменений. Тогда
ω2 = ω1 = 0,05 В/дел., Х2 = 5 В, ∆Х2 = ∆Х1 = 0,0375
В, а относительная погрешность Е2 = 0,75%. То есть второе
измерение с помощью данного прибора проделано с гораздо большей точностью.
Именно поэтому при измерениях следует ставить указатель измерений в
многопредельных приборах в такое положение, при котором стрелка оказывалась
бы как можно ближе к концу шкалы прибора (как минимум – в последней ее трети;
т.е. в зоне измерения).
Оценка погрешности
электрических измерений.
Определение наиболее выгодных условий эксперимента
Вопрос о математической обработке результатов измерения
физических величин подробно рассматривается на вводном занятии к
лабораторному практикуму «Механика и молекулярная физика». Здесь приводятся
лишь некоторые особенности оценки погрешности при измерении с помощью
электрических приборов, а также уточняется ряд основных понятий.
Вначале рассмотрим прямые электрические измерения. Если по
условиям эксперимента некоторая физическая величина измеряется несколько раз,
то абсолютная погрешность такого измерения ∆ складывается из трех
составляющих:
∆ =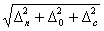 , (7) , (7)
где ∆n – погрешность, которую дает
электроизмерительный прибор; ∆c – погрешность при снятии отсчета со шкалы прибора;
∆o –
случайная погрешность.
Первое слагаемое определяется классом точности прибора, и
его величина зависит от величины ∆Х, которая вычисляется по (5).
Физическая сущность этого параметра пояснена в разделе 4. Учитывая, что при
выполнении лабораторных работ требуется, чтобы доверительная вероятность Р = 0,95, для вычисления ∆n необходимо пользоваться
следующим соотношением:
 , (8) , (8)
где ∆Х рассчитывается по
(5).
Вторая составляющая связана с неизбежным округлением показаний
электроизмерительных приборов при снятии отсчета со шкалы. Эта погрешность
может быть оценена при Р=0,95 по формуле
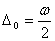 ,
(9) ,
(9)
где 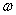 – цена деления
равномерной шкалы прибора, вычисляемая по (1). – цена деления
равномерной шкалы прибора, вычисляемая по (1).
При выполнении работ в лаборатории электричества и магнетизма
часто приходится ограничиваться однократными измерениями физических величин.
В первую очередь это касается измерения параметров электрической цепи (силы
тока, напряжения и др.) Вместо (7) для определения абсолютной погрешности
однократного измерения (∆1) используют более простую
формулу, в которую входят только два первых слагаемых (∆n и ∆o):
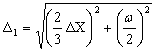 . (10) . (10)
Третье слагаемое в (7) учитывается только в том случае,
если физическая величина была измерена несколько раз. Расчет его производится
по методу Стьюдента:
 , (11) , (11)
где tpn –
коэффициент Стьюдента; S
– средняя квадратичная погрешность серии измерений. В любом случае, если одно
из слагаемых (7) значительно (на порядок) больше двух других, эти последние
не учитываются.
При косвенных измерениях (с которыми мы, как правило, и
будем иметь дело) оценку абсолютной погрешности следует производить,
используя схему вычислений, подробно рассмотренную на вводном занятии к
лабораторному практикуму «Механика и молекулярная физика». Здесь на
конкретном примере напомним лишь алгоритм этой схемы.
Найдем относительную и абсолютную погрешности при определении
горизонтальной составляющей напряженности магнитного поля Земли (лабораторная
работа № 40). Рабочая формула для определения горизонтальной составляющей Н
выглядит следующим образом:
 , (12) , (12)
где I – сила тока в цепи; n – число витков тангенс-гальванометра; r – радиус витков; 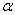 – угол отклонения
магнитной стрелки. – угол отклонения
магнитной стрелки.
Согласно упомянутой схеме вычисления, необходимо вначале
прологарифмировать рабочую формулу (12):
lnH = lnI + lnn - ln2 – lnr - ln tgα . (13)
Затем выражение (13) продифференцировать, учитывая, что
«n» и «2» – величины постоянные:
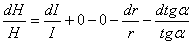 . (14) . (14)
Последнее слагаемое в (14) продифференцируем отдельно:
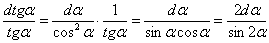 . .
Далее в (14) заменяем знаки «минус» на
«плюс», а дифференциалы dH, dI,dr и
dα – на значения абсолютных погрешностей ∆H, ∆I, ∆r, ∆α:
Е =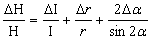 . (15) . (15)
Поскольку отношение ∆Н/Н является относительной
погрешностью E измерения горизонтальной составляющей напряженности магнитного
поля Земли, то формула (15) используется для вычисления Е.
Определив Е = ΔН/Н, находят ∆Н – абсолютную погрешность
этого измерения: ∆Н = НЕ, причем Н рассчитывают по (12).
Окончательный результат измерения дают в виде Н ±
∆Н. Таков алгоритм расчета.
Для того чтобы рассчитать Е по
(15), необходимо вычислить погрешности прямых измерений ∆H, ∆I, ∆r, ∆αх (величина I непосредственно
измеряется амперметром, r
– линейкой, α –
по круговой шкале компаса тангенс-гальванометра). Эти вычисления проделывают
следующим образом.
Погрешность прямого измерения ∆ I в общем случае рассчитывается по
формулам (7)-(11). Однако в данной лабораторной работе производится однократное
измерение силы тока, поэтому воспользуемся упрощенной формулой (10),
подставив вместо ∆Х его выражение из (5):
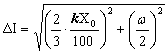 . (16) . (16)
Все используемые ниже числовые данные взяты произвольно и
не являются реальными параметрами лабораторной работы № 40.
Пусть величина тока определяется амперметром, класс точности
которого k = 0,5, предел измерения Хо = I А, полное число делений
на шкале N = 200, т.
е. цена деления согласно (1)
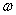 = 0,005А. Подставив
числовые данные в (16), получим = 0,005А. Подставив
числовые данные в (16), получим
∆ I = 0,003 А.
Погрешность ∆r – это погрешность однократного измерения, поэтому в (7)
∆c =
0; кроме того, измерение r
производится не электроизмерительным прибором, поэтому ∆n = 0. Следовательно,
∆r
определяется только величиной ∆o, т.е. из (7) получаем соотношение (9), которым и
воспользуемся для оценки ∆r:
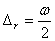 , (17) , (17)
где 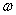 – цена
деления шкалы прибора, которым измеряем r. – цена
деления шкалы прибора, которым измеряем r.
Пусть измерения производились линейкой, деления которой
нанесены через 1 см
(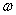 = 0,01
м). Подставив в (17), получим = 0,01
м). Подставив в (17), получим
∆r =
0,005 м.
Погрешность ∆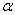 тоже рассчитывается по (17). Пусть деления на шкале
компаса тангенс-гальванометра нанесены через 20,
т. е. через 0,035 радиан ( тоже рассчитывается по (17). Пусть деления на шкале
компаса тангенс-гальванометра нанесены через 20,
т. е. через 0,035 радиан (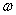 = 0,035 рад). Подставив в (17), получим ∆ = 0,035 рад). Подставив в (17), получим ∆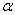 = 0,0175 рад. = 0,0175 рад.
Если, например, амперметр показывает силу тока в цепи
I = 0,95 А, радиус витков r = 0,25 м, а угол отклонения
стрелки
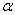 = 45°,
то с учетом полученных выше величин = 45°,
то с учетом полученных выше величин 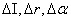 по (15) вычислим значение относительной погрешности: E = 0,058 или 5,8%. по (15) вычислим значение относительной погрешности: E = 0,058 или 5,8%.
Горизонтальная составляющая напряженности магнитного поля
Земли, вычисленная по этим данным из формулы (12), имеет величину Н = 13,3 А/м (если принять число витков n = 7).
Поэтому абсолютная
погрешность 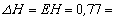 0,8 А/м, и окончательный результат
измерения (13,3 ± 0,8) А/м, с доверительной вероятностью 0,95. 0,8 А/м, и окончательный результат
измерения (13,3 ± 0,8) А/м, с доверительной вероятностью 0,95.
На этом примере можно показать, что формула типа (15), полученная
для расчета погрешности, может использоваться для определения наиболее
выгодных условий эксперимента. В данной формуле величина относительной
погрешности измерения силы тока (первое слагаемое) будет зависеть от класса
точности и правильности выбора предела измерения амперметра. Второе слагаемое
тем меньше, чем точнее прибор, которым измеряют радиус кругового контура с
током. Что же касается третьего слагаемого, то оно имеет наименьшую величину
при максимальном значении знаменателя 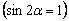 , т.е. при α
= 45°. , т.е. при α
= 45°.
Следовательно, наиболее выгодными условиями эксперимента
будут следующие: 1) угол отклонения магнитной стрелки при включении
электрического тока близок к 45°; 2) предел измерения амперметра выбран так, что при
отклонении магнитной стрелки на угол ~45° стрелка амперметра
находится в пределах последней трети его шкалы.
Заметим, что в общем случае при косвенных измерениях условия
минимума относительной погрешности не всегда находятся легко. Но во многих
случаях это оказывается возможным, и анализ полученной формулы [типа (15)]
дает полезную информацию об условиях проведения эксперимента.
Контрольные вопросы
2.
Как выбирать нужный предел измерения у многопредельного
прибора?
3.
Что такое цена деления? Как находят численное
значение измеряемой величины по отклонению стрелки многопредельного прибора?
4.
По обозначениям на шкале данного прибора расскажите
об условиях его эксплуатации, назначении, принципе действия, оцените его
точность.
5.
Что такое класс точности прибора? При каких условиях
относительная погрешность при измерении данным прибором минимальна?
7.
Каков алгоритм расчета относительной и абсолютной погрешностей
при косвенных измерениях (на предложенном примере)? Для чего их определяют?
Как записывается окончательный результат измерения?
8.
Определите наиболее выгодные условия проведения эксперимента
в данной лабораторной работе.
|
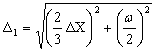 .
. 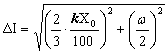 .
.